When we talk about algorithms, one of the first things that comes up is Big O Notation.
But what exactly is it, and why should you care?
In simple terms, Big O Notation helps us describe how the performance of an algorithm changes as the size of the input grows. It gives us a way to talk about how fast or how slow our code is — not in seconds, but in terms of growth.
In this article, we’ll cover:
- What Big O Notation means (in plain English)
- The most common Big O complexities you’ll run into
- Simple, real-world examples to make each concept stick
- Why understanding Big O matters for developers
By the end of this post, you'll have a clear understanding of Big O, and you’ll be able to spot performance issues (and brag about it in code reviews 😉).
Let’s dive in! 🧑💻✨
📚 What is Big O Notation?
Big O Notation is a way to describe the efficiency of an algorithm by focusing on how its running time or space requirements grow relative to the input size.
It doesn’t measure time in seconds or memory in megabytes.
Instead, it provides a high-level understanding of how scalable an algorithm is.
Take a quick look at how different complexities grow visually:
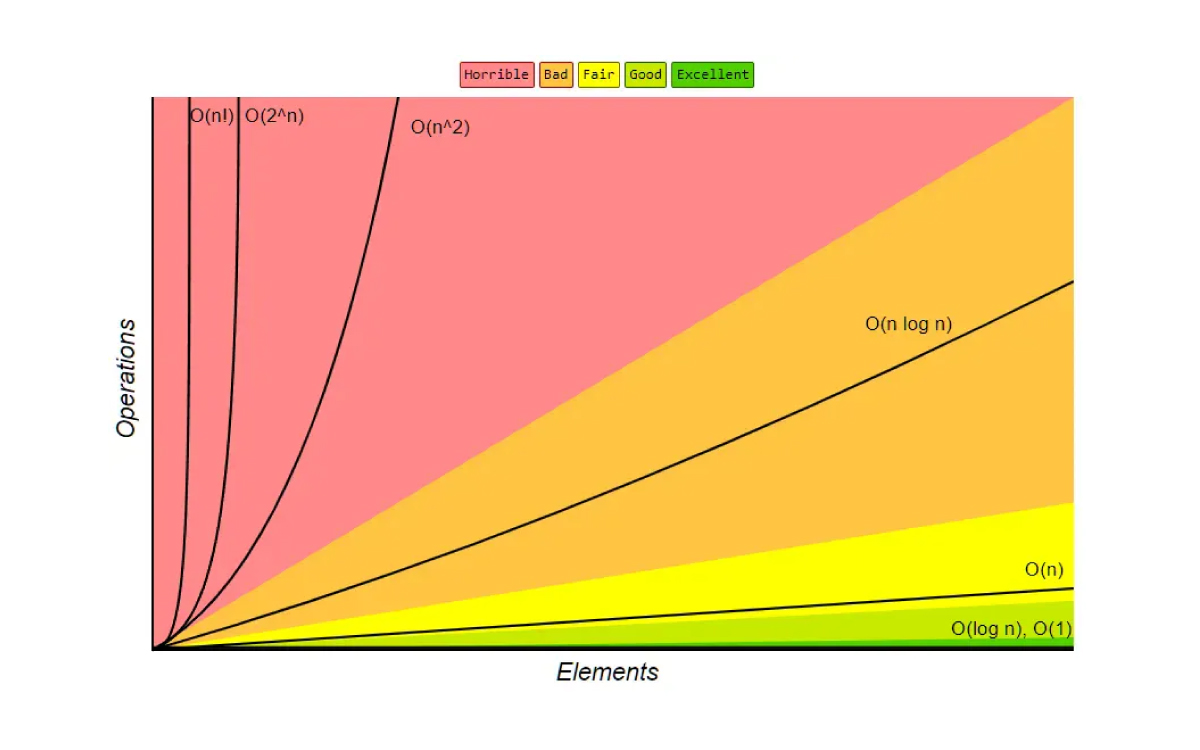
Think of it like this:
- How much slower will your program get if the input doubles?
- Will it still run smoothly with 10x more data?
- Will it completely crash and burn?
Big O helps us answer these questions before we ship slow code into production.
🧠 Why Big O Matters
You might wonder: "My code runs fine, why should I care?"
Here’s why:
- Scalability: As the data grows, poorly optimized code can become painfully slow.
- Interviews: Big O analysis is a major focus in technical interviews, sometimes.
- Better decision making: Knowing which algorithm to pick can save you tons of headaches.
- Code quality: Writing efficient code is part of writing good code.
In short: understanding Big O makes you a better developer. 💪
🛠 Common Big O Complexities (With Examples)
Here are some of the most common Big O complexities you’ll see in real life:
O(1) — Constant Time
The algorithm takes the same amount of time, no matter the input size.
Example:
function getFirstItem(arr) {
return arr[0];
}- Getting the first element of an array is always a quick operation.
O(log n) — Logarithmic Time
The running time grows slowly even as input size increases dramatically.
Example: Binary Search
function binarySearch(arr, target) {
let left = 0;
let right = arr.length - 1;
while (left <= right) {
let middle = Math.floor((left + right) / 2);
if (arr[middle] === target) {
return middle;
} else if (arr[middle] < target) {
left = middle + 1;
} else {
right = middle - 1;
}
}
return -1;
}Binary search is super efficient — cutting the search space in half each time!
O(n) — Linear Time
The algorithm’s running time grows linearly with the input size.
Example:
function printAllItems(arr) {
for (let item of arr) {
console.log(item);
}
}Looping through all items once is O(n) — double the items, double the time.
O(n log n) — Linearithmic
Example: Merge Sort
function mergeSort(arr) {
if (arr.length <= 1) return arr;
const middle = Math.floor(arr.length / 2);
const left = mergeSort(arr.slice(0, middle));
const right = mergeSort(arr.slice(middle));
return merge(left, right);
}
function merge(left, right) {
const result = [];
while (left.length && right.length) {
if (left[0] < right[0]) result.push(left.shift());
else result.push(right.shift());
}
return result.concat(left, right);
}- Why O(n log n): The array is divided in half each time (log n splits), and at each level, all elements are merged (n work).
O(n²) — Quadratic Time
The running time grows exponentially with the input size.
Example:
function printAllPairs(arr) {
for (let i of arr) {
for (let j of arr) {
console.log(i, j);
}
}
}- This function will iterate n*n times, which is, j times of array each i time of array.
- Nested loops over the same array → bad news for large inputs!
O(2ⁿ) — Exponential
Example: Recursive Fibonacci
function fibonacci(n) {
if (n <= 1) return n;
return fibonacci(n - 1) + fibonacci(n - 2);
}- Why O(2ⁿ): Each call spawns two more calls, leading to exponential growth.
O(n!) — Factorial
Example: Brute-force Permutations
Brute-force permutations are a method of generating all possible arrangements of a given set of elements. This technique generally has a time complexity of O(n!) because, for a set of n elements, there are n! (factorial of n) possible permutations.
function permute(arr) {
if (arr.length <= 1) return [arr];
const result = [];
for (let i = 0; i < arr.length; i++) {
const current = arr[i];
const remaining = arr.slice(0, i).concat(arr.slice(i + 1));
const remainingPermuted = permute(remaining);
for (const perm of remainingPermuted) {
result.push([current].concat(perm));
}
}
return result;
}- Why O(n!): For an array of n elements, there are n! possible permutations to explore.
📊 Quick Visual Reference
| Big O | Name | Example |
|---|---|---|
| O(1) | Constant | Accessing array by index |
| O(log n) | Logarithmic | Binary Search |
| O(n) | Linear | Loop through array |
| O(n log n) | Linearithmic | Efficient sorting algorithms (like Merge Sort, Quick Sort) |
| O(n²) | Quadratic | Nested loops |
| O(2ⁿ) | Exponential | Recursive Fibonacci calculation |
| O(n!) | Factorial | Brute-force Permutations |
📝 Final Thoughts
Big O Notation isn’t just for whiteboard interviews.
It’s a practical tool that helps you write better, faster, and more scalable code.
You don’t always have to optimize everything for the best Big O — but knowing when an algorithm will fall apart under pressure gives you a major advantage.
Thanks for reading! 🙌
Feel free to drop a comment if you have any questions or want to share your favorite Big O example!