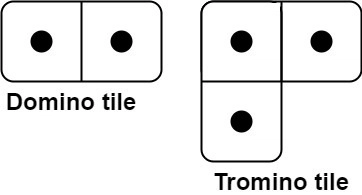
790. Domino and Tromino Tiling

Difficulty: Medium

Topics: Dynamic Programming

You have two types of tiles: a 2 x 1 domino shape and a tromino shape. You may rotate these shapes.
lc-domino

Given an integer n, return the number of ways to tile an 2 x n board. Since the answer may be very large, return it modulo 109 + 7.

In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.

Example 1:

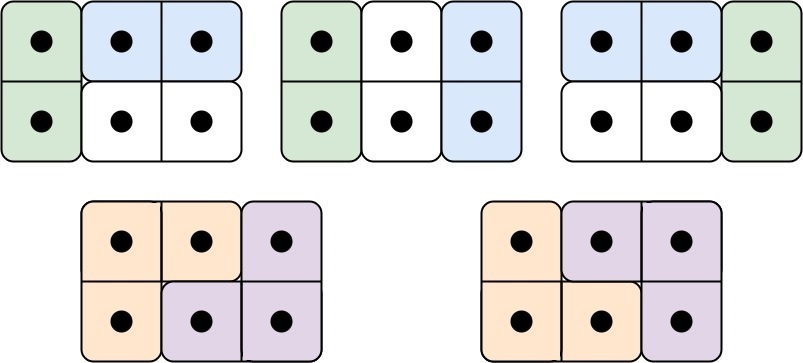
lc-domino1

  • Input: n = 3
  • Output: 5
  • Explanation: The five different ways are show above.

Example 2:

  • Input: n = 1
  • Output: 1

Example 3:

  • Input: n = 2
  • Output: 2

Example 4:

  • Input: n = 4
  • Output: 11

Example 5:

  • Input: n = 5
  • Output: 24

Constraints:

  • 1 <= n <= 1000

Solution:

We need to determine the number of ways to tile a 2xN board using dominoes and trominoes. The solution involves dynamic programming to efficiently compute the number of valid tilings.

Approach

The key insight is to recognize the recurrence relation that captures the number of ways to tile the board up to a given length. The recurrence relation is derived based on the different ways tiles can be added to extend the tiling from smaller boards to larger ones. The recurrence relation is:

  • dp[n] = 2 * dp[n-1] + dp[n-3]

This relation accounts for:

  1. Adding a vertical domino to a tiling of length n-1.
  2. Adding two horizontal dominoes to a tiling of length n-2.
  3. Adding trominoes in configurations that require considering tilings of length n-3.

Let's implement this solution in PHP: 790. Domino and Tromino Tiling

/**
 * @param Integer $n
 * @return Integer
 */
function numTilings($n) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Example usage
echo numTilings(3); // Output: 5
echo numTilings(1); // Output: 1
echo numTilings(2); // Output: 2
echo numTilings(4); // Output: 11
echo numTilings(5) // Output: 24
?>

Explanation:

  1. Base Cases:

    • dp[0] = 1: An empty board has one way to be tiled (doing nothing).
    • dp[1] = 1: A 2x1 board can only be tiled with one vertical domino.
    • dp[2] = 2: A 2x2 board can be tiled with two vertical dominoes or two horizontal dominoes.

  2. Recurrence Relation:

    • For n >= 3, the number of ways to tile a 2xn board is derived from the formula dp[n] = 2 * dp[n-1] + dp[n-3]. This formula accounts for:
      • Adding a vertical domino to a tiling of length n-1.
      • Adding two horizontal dominoes to a tiling of length n-2 (implicitly handled through the dynamic programming approach).
      • Adding configurations involving trominoes that extend from a tiling of length n-3.

  3. Modulo Operation:

    • Since the result can be very large, we take modulo 10^9 + 7 at each step to prevent overflow and ensure the result fits within standard integer limits.

This approach efficiently computes the number of tilings using dynamic programming, ensuring optimal time complexity of O(n) and space complexity of O(n).

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks 😍. Your support would mean a lot to me!

If you want more helpful content like this, feel free to follow me: