This is a Plain English Papers summary of a research paper called AI Learns General Reasoning: Nemotron-CrossThink Beats Math-Only LLMs. If you like these kinds of analysis, you should join AImodels.fyi or follow us on Twitter.
Breaking the Math Barrier: How Nemotron-CrossThink Extends LLM Self-Learning to General Reasoning
Large Language Models (LLMs) have shown impressive reasoning capabilities when enhanced through Reinforcement Learning (RL). While applying RL to math reasoning has been successful due to well-defined rules and verifiable answers, extending these techniques to broader domains presents significant challenges. Diverse reasoning tasks demand different cognitive approaches and reward structures, making it difficult to design effective RL training that generalizes beyond mathematics.
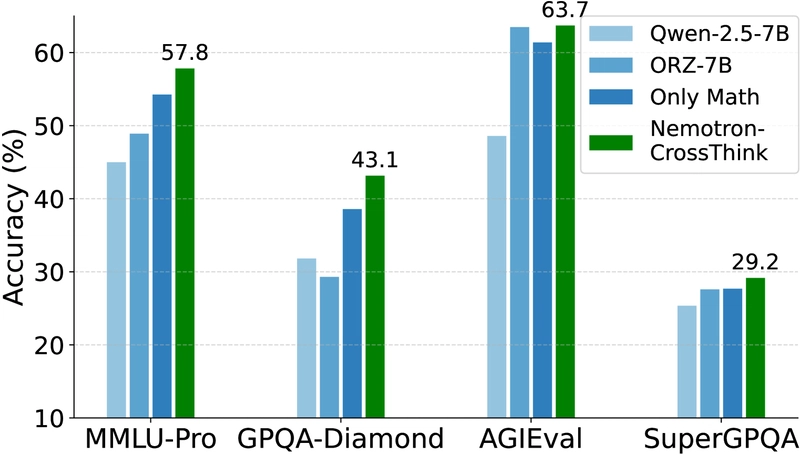
Figure 1: Performance comparison showing Nemotron-CrossThink outperforming math-only training and existing reasoners on diverse benchmarks.
In this research, NVIDIA and Carnegie Mellon researchers introduce Nemotron-CrossThink, a framework that systematically incorporates multi-domain corpora into RL training to improve generalization across diverse reasoning tasks. The approach addresses key challenges by incorporating data from varied domains, applying structured templates to control answer-space complexity, filtering for verifiable answers, and optimizing data blending strategies.
The Nemotron-CrossThink Framework
Nemotron-CrossThink offers a systematic way to incorporate multi-domain data for self-learning that results in better generalization across diverse tasks:

Figure 2: The Nemotron-CrossThink pipeline showing data curation, templating, filtering, and RL training steps.
The framework consists of four main components:
Data Curation: Collecting diverse data from synthetic sources (Common Crawl) and open-source QA datasets spanning STEM, humanities, law, and social sciences.
Template Application: Converting questions into multiple-choice (MCQ) and open-ended formats to promote diverse reasoning trajectories.
Data Filtering: Removing samples that can't be verified with rule-based rewards.
Data Blending: Optimizing the mix of data from different domains and formats.
This process culminates in reinforcement learning using Group Relative Policy Optimization (GRPO) to refine reasoning capabilities across diverse domains.
Building a Diverse Training Dataset
The researchers curated a dataset combining both synthetically generated data and open-source QA pairs, categorized into general-purpose reasoning (GPR) and mathematical reasoning (MR):
| Data Source | Category | Type | Samples |
|---|---|---|---|
| MMLU [Train] | GPR | MCQ | 99,842 |
| Syn-QA | GPR | MCQ | 192,950 |
| Natural Reasoning | GPR | OE | 100,000 |
| NuminaMath | MR | OE | 87,350 |
| PersonaSkill-MATH | MR | OE | 100,000 |
| Math | MR | OE | 8523 |
| Total | 588,645 |
Table 1: Training data distribution showing the mix of general-purpose and mathematical reasoning sources in multiple-choice and open-ended formats.
For general-purpose reasoning (GPR), they collected open-source datasets like Natural Reasoning and MMLU training set, spanning multiple domains including STEM fields, economics, and social sciences. They also synthesized additional QA pairs from Common Crawl documents (Syn-QA).
For mathematical reasoning (MR), they incorporated established datasets like MATH and NuminaMath, along with synthetic math problems generated using the PersonaSkill method.
Controlling Answer Space Through Templates
Since different question types elicit different reasoning patterns, the researchers applied two templates to their data:
- Multiple-Choice Questions (MCQ): Presenting fixed options for selection.
- Open-Ended Questions: Requiring the model to generate answers without options.
This templating approach allows for verifiable rewards in non-deterministic domains by limiting the answer space, making it feasible to apply reinforcement learning beyond math.
Strategic Data Blending for Optimal Performance
After gathering diverse datasets, the researchers explored different blending strategies to understand how domain and format diversity affect model performance:
| Category | Blend Name | Symbol | Blend Description |
|---|---|---|---|
| Data Source | Natural Distribution | $B_{nd}$ | Ratio of number of samples in a dataset divided by the total number of samples in all the datasets. |
| More Math | $B_{mr↑}$ | 2:1 ratio of $\mathcal{D}{mr}$ and $\mathcal{D}{gpr}$ | |
| More General Purpose Reasoning | $B_{gpr↑}$ | 2:1 ratio of $\mathcal{D}{gpr}$ and $\mathcal{D}{mr}$ | |
| Question Types | More MCQ | $B_{mcq↑}$ | 2:1 ratio of $\mathcal{D}{mcq}$ and $\mathcal{D}{open}$ |
| More Open-Ended | $B_{open↑}$ | 2:1 ratio of $\mathcal{D}{open}$ and $\mathcal{D}{mcq}$ | |
| Data Usefulness | Avg. Score | $B_{score}$ | Provide weight to each source based on their average benchmark performances |
Table 2: Overview of data blending strategies, categorized by data source, question type, and data usefulness.
These blending strategies were designed to test hypotheses about how domain diversity and question format affect reinforcement learning outcomes. For comparison, the researchers also created two single-source blends: one using only math data ($B_{only_mr}$) and one using only general-purpose reasoning data ($B_{only_gpr}$).
Experimental Setup
The researchers used Qwen2.5-7B and Qwen2.5-32B as their baseline models, applying GRPO training using the veRL framework. They evaluated model performance on diverse benchmarks including:
- Math benchmarks: MATH-500, AMC23
- General-purpose reasoning benchmarks: MMLU, MMLU-PRO, AGIEVAL, GPQA-DIAMOND, and SUPERGPQA
This comprehensive evaluation ensured the results generalized across various reasoning domains, not just mathematical ones.
Individual Dataset Impact
To understand which datasets contribute most to reasoning performance, the researchers first trained models on individual datasets:
| Data Source | MMLU | MMLU-PRO | GPQA-DIAMOND | AGIEVAL | SUPERGPQA | MATH-500 | AMC23 | Avg |
|---|---|---|---|---|---|---|---|---|
| $\mathcal{M}$ | 74.20 | 45.00 | 31.82 | 48.59 | 25.36 | 48.30 | 40.00 | 44.75 |
| MMLU [Train] | 69.76 | 38.50 | 32.83 | 47.66 | 27.69 | 22.00 | 5.00 | 34.78 |
| Syn-QA | 70.45 | 52.41 | 30.81 | 52.10 | 24.57 | 54.20 | 35.00 | 45.65 |
| Natural Reasoning | 68.89 | 31.33 | 33.33 | 46.65 | 22.44 | 68.60 | 42.50 | 44.82 |
| NuminaMath | 72.94 | 52.05 | 33.84 | 54.39 | 26.97 | 76.20 | 55.00 | 53.06 |
| PersonaSkill-Math | 53.99 | 28.08 | 18.69 | 45.69 | 16.92 | 77.20 | 50.00 | 41.51 |
| Math | 63.30 | 31.64 | 21.72 | 51.95 | 18.31 | 78.40 | 50.00 | 45.04 |
Table 3: Results of self-learning on individual datasets, showing their varying strengths across different benchmarks.
The analysis revealed several insights:
- NuminaMath achieved the highest overall average, outperforming the baseline by over 8.3%, with strong performance on both math and general-purpose reasoning tasks.
- Syn-QA showed modest improvement over the baseline with stronger accuracy in MMLU-PRO and AGIEVAL.
- MMLU [Train] performed best on SUPERGPQA, suggesting it captures broad conceptual knowledge useful for long-tail domains.
- Natural Reasoning showed surprisingly good math performance despite being a GPR dataset.
These results informed the data blending strategy for maximum effectiveness.
Performance Across Blending Strategies
Next, the researchers compared the performance of different blending strategies:
| Model | Category | Blend | MMLU | MMLU-PRO | GPQA-DIAMOND | AGIEVAL | SUPERGPQA | MATH-500 | AMC23 | Avg |
|---|---|---|---|---|---|---|---|---|---|---|
| $\mathcal{M}$ | 74.20 | 45.00 | 31.82 | 48.59 | 25.36 | 48.30 | 40.00 | 44.75 | ||
| ORZ | 73.20 | 48.90 | 29.30 | 63.49 | 27.60 | 81.40 | 62.50 | 55.20 | ||
| *CrossThink | Data Source | $B_{nd}$ | 73.18 | 54.81 | 38.07 | 59.99 | 26.54 | 77.00 | 60.00 | 55.66 |
| $B_{mr↑}$ | 74.85 | 55.51 | 40.10 | 61.47 | 26.81 | 77.80 | 67.50 | 57.72 | ||
| $B_{gpr↑}$ | 74.94 | 57.82 | 38.58 | 63.71 | 29.16 | 77.60 | 65.00 | 58.12 | ||
| Question Types | $B_{mcq↑}$ | 74.26 | 55.77 | 39.59 | 62.54 | 28.05 | 78.00 | 60.00 | 56.89 | |
| $B_{open↑}$ | 74.46 | 55.82 | 43.15 | 61.28 | 26.82 | 78.40 | 62.50 | 57.49 | ||
| Data Usefulness | $B_{score}$ | 74.70 | 56.16 | 40.10 | 59.80 | 27.37 | 78.00 | 62.50 | 56.95 | |
| Single Source | $B_{only_mr}$ | 74.24 | 54.26 | 38.58 | 61.39 | 27.69 | 78.60 | 70.00 | 57.82 | |
| $B_{only_gpr}$ | 72.77 | 52.06 | 37.06 | 56.56 | 27.44 | 72.20 | 55.00 | 53.30 |
Table 4: Results showing Nemotron-CrossThink-7B performance across different blending strategies. The multi-domain blend $B_{gpr↑}$ achieves the highest overall average.
Key findings include:
- All blending strategies significantly outperformed the base model.
- $B_{gpr↑}$ (emphasizing general-purpose reasoning) achieved the highest overall average (58.12%), outperforming Open-Reasoner-Zero (ORZ) by ~5%.
- While $B_{only_mr}$ (math-only training) performed slightly better on math-specific tasks, it lagged behind on general reasoning benchmarks.
- $B_{open↑}$ (emphasizing open-ended questions) outperformed $B_{mcq↑}$ (emphasizing multiple-choice questions).
These results demonstrate that integrating diverse reasoning domains in RL leads to better overall performance than domain-specific training.
Token Efficiency: Doing More with Less
Beyond accuracy, the researchers analyzed how different training strategies affect the verbosity and efficiency of model responses:
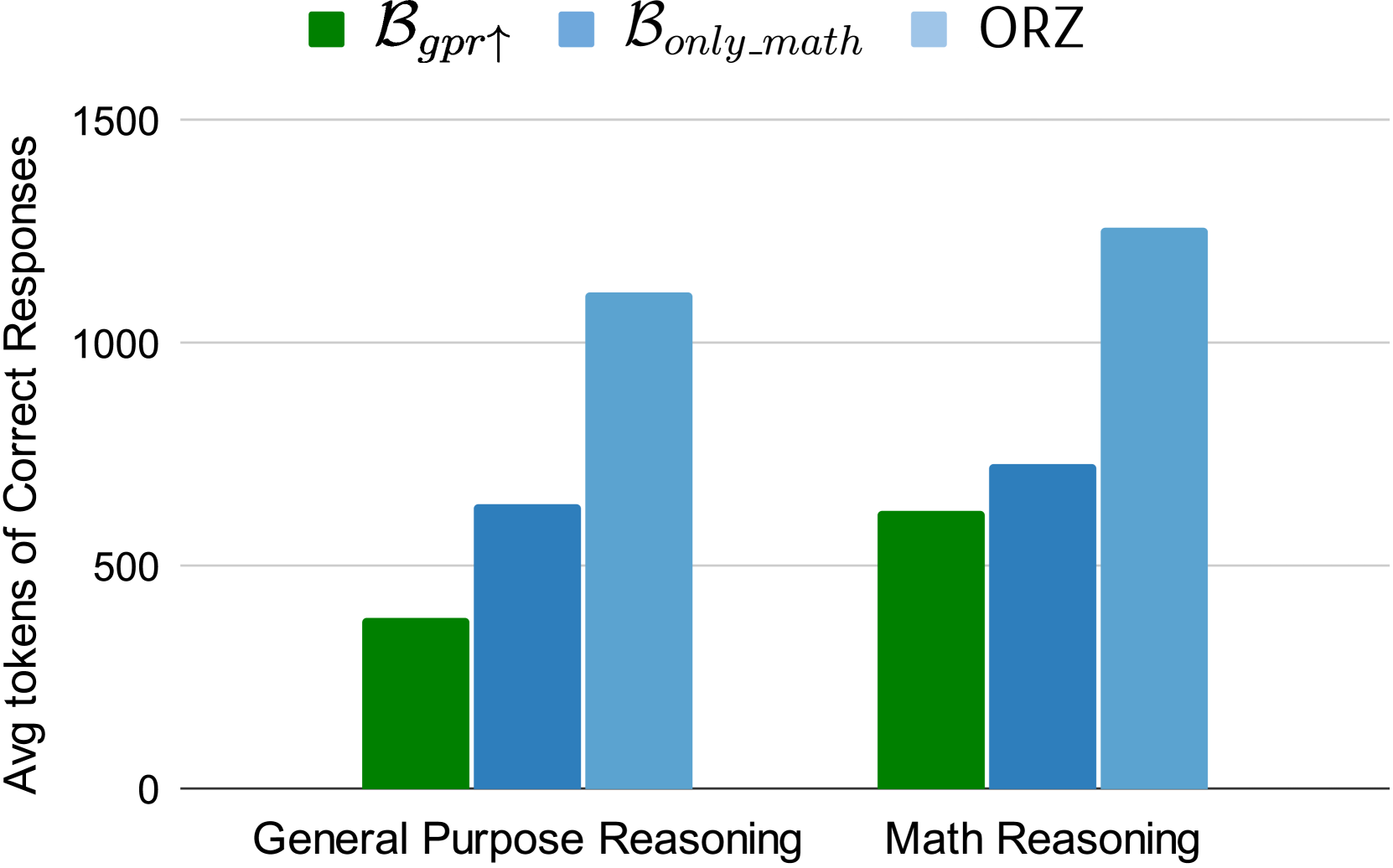
Figure 3: Token efficiency comparison showing that multi-domain training ($B_{gpr↑}$) leads to more concise responses than math-only training.
On general-purpose reasoning benchmarks, models trained with the multi-domain blend ($B_{gpr↑}$) produced correct answers with significantly fewer tokens than math-only models. For instance, on MMLU, $B_{gpr↑}$ used an average of 229 tokens for correct responses, compared to 351 for $B_{only_mr}$.
Interestingly, on math benchmarks, $B_{gpr↑}$ appropriately generated longer responses, adapting its verbosity to the task requirements. This adaptive behavior highlights a key strength of multi-domain training: it equips the model with the flexibility to tailor its response style to the nature of the task.
Across all tasks, the multi-domain model used 28% fewer tokens on average for correct responses than the math-only model, demonstrating more efficient reasoning.
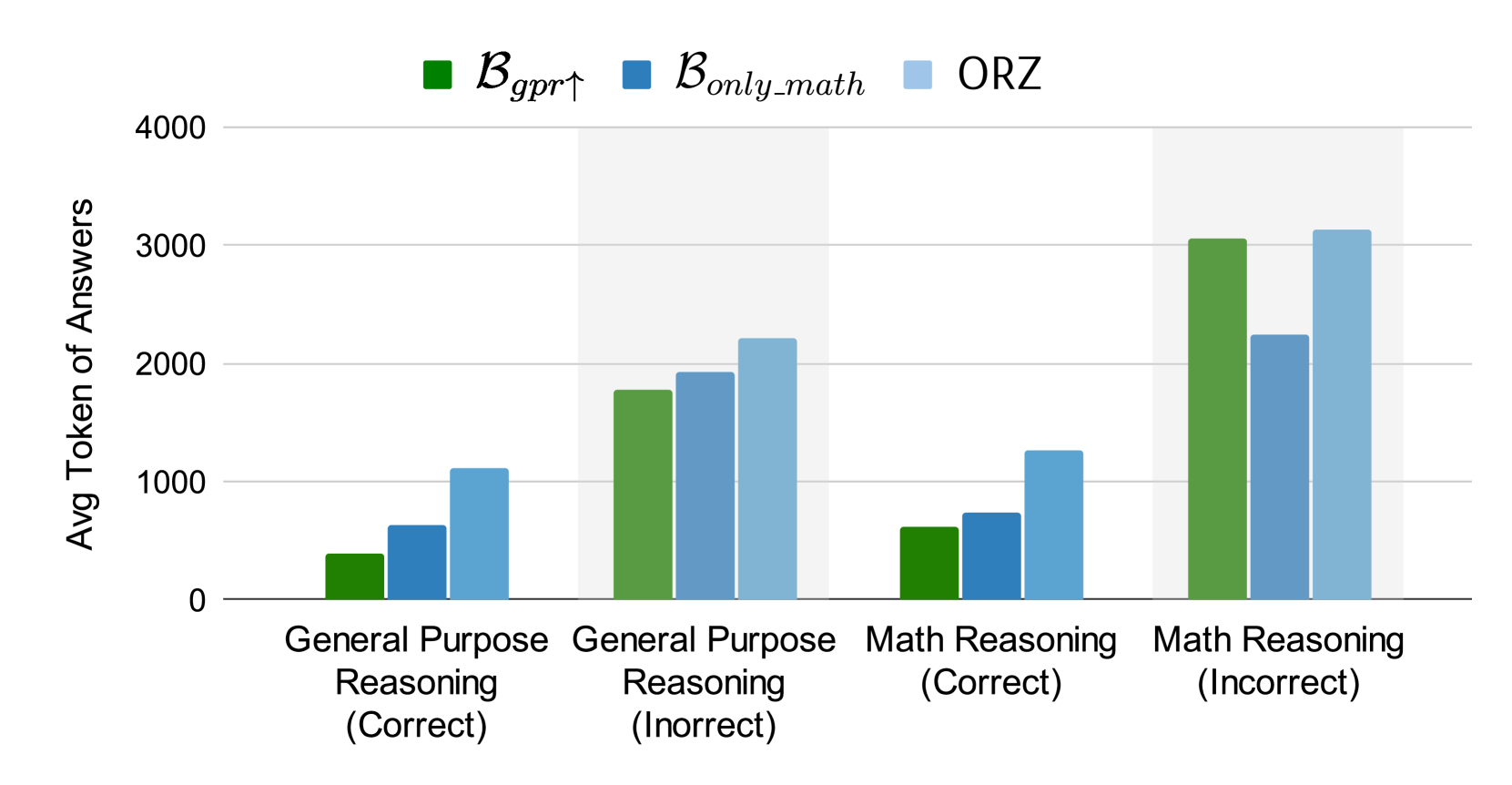
Figure 4: Comparison showing incorrect responses are consistently longer than correct ones, suggesting verbose reasoning doesn't guarantee correctness.
The analysis also revealed that incorrect responses are substantially longer than correct ones—by 3.6× on average. This suggests that verbose reasoning often reflects model uncertainty or repetitive thinking rather than productive deduction.
Data Format Study: Question and Answer Templates
The researchers investigated how question and answer formats affect model performance:
| Question Type | MMLU | MMLU-PRO | GPQA-DIAMOND | AGIEVAL | SUPERGPQA | MATH-500 | AMC23 | Avg |
|---|---|---|---|---|---|---|---|---|
| MCQ +OPEN-ENDED | 73.18 | 54.81 | 38.07 | 59.99 | 26.54 | 77.00 | 60.00 | 55.66 |
| OPEN-ENDED | 74.61 | 54.36 | 39.09 | 59.30 | 29.16 | 76.60 | 65.00 | 56.87 |
Table 5: Impact of Question Format. Converting all questions to open-ended format improves accuracy across benchmarks, reducing reliance on option guessing and encouraging deeper reasoning.
The open-ended-only configuration outperformed the mixed-format setting across most benchmarks, achieving a 1.21% higher average score. This suggests that removing multiple-choice options forces the model to rely more on reasoning rather than potentially guessing from options.
For answer formats in multiple-choice questions, they compared short-form (option label only, e.g., "A") versus long-form answers (option label with description, e.g., "(A) The sky is blue"):
| Answer Type | MMLU | MMLU-PRO | GPQA-DIAMOND | AGIEVAL | SUPERGPQA | MATH-500 | AMC23 | Avg |
|---|---|---|---|---|---|---|---|---|
| Long | 72.77 | 52.06 | 37.06 | 56.56 | 27.44 | 72.20 | 55.00 | 53.30 |
| Short | 74.22 | 54.56 | 39.59 | 58.01 | 28.39 | 74.20 | 52.50 | 54.50 |
Table 6: Impact of Answer Format. Using short-form answers improves accuracy by reducing output ambiguity and avoiding penalization from rigid reward functions in rule-based training.
Short-form answers consistently outperformed long-form variants, with a 1.20% improvement in average accuracy. This suggests that reducing output complexity minimizes ambiguity and better aligns with rule-based reward signals.
Difficulty-Based Filtering Enhances Performance
The researchers explored a simple approach to estimate question difficulty for datasets without explicit difficulty labels. They labeled questions as "difficult" if they were answered incorrectly by a smaller model (Qwen-2.5-7B) in a zero-shot setting:
| Model | Blend | MMLU | MMLU-PRO | GPQA-DIAMOND | AGIEVAL | SUPERGPQA | MATH-500 | AMC23 | Avg |
|---|---|---|---|---|---|---|---|---|---|
| Qwen-2.5-32B | 83.30 | 55.10 | 40.40 | 62.77 | 33.16 | 60.55 | 45.00 | 54.33 | |
| NEMOTRON-CROSSTHINK-32B | $\mathcal{B}_{gpr↑}$ | 83.57 | 68.83 | 46.70 | 73.90 | 37.99 | 82.40 | 67.50 | 65.84 |
| $B_{f(gpr)↑}$ | 83.60 | 69.43 | 49.75 | 75.82 | 38.34 | 84.00 | 75.00 | 67.99 |
Table 7: Difficulty-Based Filtering results showing that training on harder examples yields consistent gains across all benchmarks.
This filtering approach resulted in consistent performance improvements across all benchmarks. While both filtered and unfiltered models outperformed the original baseline, the model trained on the filtered dataset achieved the highest accuracy on every task. On average, filtering boosted overall accuracy by 2.15%, suggesting that selectively training on challenging examples produces more robust and generalizable models.
Broader Implications
Nemotron-CrossThink demonstrates that data diversity, not just volume, is key to broader reasoning capabilities in language models. By combining data from diverse domains and applying thoughtful formatting strategies, the framework enables consistent gains across both general-purpose and mathematical benchmarks.
The research also shows that properly designed RL can extend beyond mathematics to general reasoning tasks, provided that appropriate templates and filtering techniques are applied to manage answer-space complexity.
Perhaps most importantly, the models trained with Nemotron-CrossThink show adaptive behavior—generating concise answers for general-purpose questions and more detailed responses for math problems—reducing inference costs while preserving task-specific rigor.
Conclusion
Nemotron-CrossThink offers a practical framework for improving the generalization abilities of language models through reinforcement learning with multi-domain corpora. By systematically addressing the challenges of applying RL beyond mathematical reasoning, it achieves substantial improvements across diverse benchmarks.
The research demonstrates that incorporating diverse reasoning domains in reinforcement learning leads to more accurate, efficient, and generalizable language models. This paves the way for future work in self-learning systems that can reason effectively across the full spectrum of human knowledge domains.