This is a Plain English Papers summary of a research paper called AI Learns Vocal Effects: Differentiable Model Matches Pro Mixing Techniques. If you like these kinds of analysis, you should join AImodels.fyi or follow us on Twitter.
Understanding Vocal Effects in Music Production
Professional music producers and audio engineers craft the sound of vocals through careful application of audio effects. These techniques shape a sound's timbre and spatial characteristics but are typically based on years of experience rather than systematic tracking. Introducing DiffVox, a novel and interpretable model for matching vocal effects in music production. DiffVox, short for "Differentiable Vocal Fx," integrates parametric equalization, dynamic range control, delay, and reverb with efficient differentiable implementations that enable gradient-based optimization for parameter estimation.
The model focuses on vocals because they're often the most prominent element in a mix and receive careful processing. Through differentiable modeling, DiffVox can capture the parameters that professional engineers use, creating a dataset of real-world vocal processing techniques.
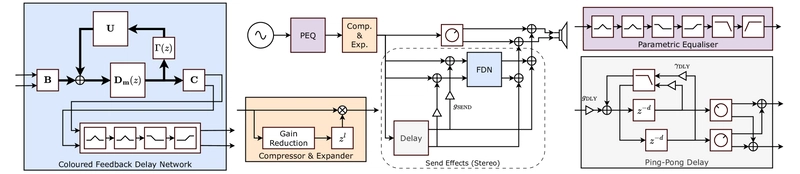
The DiffVox model architecture showing a parametric equalizer, dynamic range controller, ping-pong delay, and FDN reverb.
Inside DiffVox: A Differentiable Vocal Effects Chain
DiffVox implements a complete vocal processing chain similar to what professionals use. The mono input first passes through a parametric equalizer, then a compressor and expander, before splitting into parallel paths for dry and wet signal processing with spatial effects. This creates a powerful yet compact representation specific to vocal processing.
The Parametric Equalizer
The model implements a six-band parametric equalizer with two peak filters, low-shelf, high-shelf, low-pass, and high-pass filters. To make recursive filtering operations more efficient, DiffVox uses Blelloch's parallel prefix sum algorithm, reducing time complexity from O(N) to approximately O(N/p), where p is the number of parallel processors. This approach enables faster computation on GPUs, which is vital for the gradient-based optimization process when estimating audio effects parameters.
The Dynamic Range Controller
DiffVox implements a feed-forward compressor and expander with look-ahead capability through truncated sinc interpolation. This approach allows precise control over the gain reduction timing, which is crucial for accurate dynamic processing. The effect is controlled by parameters including compressor/expander thresholds, ratios, attack/release times, and make-up gain.
Creating Space with Ping-Pong Delay
The model includes a differentiable ping-pong delay effect that provides stereo widening. In a ping-pong delay, the signal alternates between left and right channels with each repeat. This effect is parametrized by delay time, feedback gain, stereo spread, and a low-pass filter that can darken successive repeats - all core techniques in professional vocal production.
Adding Depth with Feedback Delay Network Reverb
For spatial depth, DiffVox implements a Feedback Delay Network (FDN) reverb with frequency-dependent decay. This approach provides a realistic sense of space while keeping the parameter count manageable. The FDN is configured to be orthogonal, ensuring energy preservation for stable reverb tails, similar to techniques used in differentiable sound rendering.
Effect Routing and Parameterization
The model includes 52 parameters across all effects, with careful parameterization to ensure stable optimization. The effects chain routes the vocal through the processing modules with additional send capability from the delay to the reverb, mimicking real-world mixing approaches.
| Condition ( $\mathbb{P}$ ) | Parametrisation $(\mathbb{R} \rightarrow \mathbb{P})$ | Parameters $(\theta \in \mathbb{R})$ |
|---|---|---|
| $x \in \mathbb{R}$ | $\theta \mapsto \theta$ | Equaliser's/make-up gain, $C T, E T, \mathbf{B}, \mathbf{C}$ |
| $0 \leq x \leq 1$ | $\sigma: \theta \mapsto \frac{1}{1+\epsilon^{2}}$ | Panning, $\alpha_{\text {rms }}, \alpha_{\text {at }}, \alpha_{\text {yt }}, E R, \gamma_{\text {DLY }}, g_{\text {DLY }}, g_{\text {SEND }}$ |
| $a \leq x \leq b$ | $\theta \mapsto a+\sigma(\theta)(b-a)$ | Equaliser's Q and frequency, $C R, d, \gamma(z)$ |
| $0 \leq x \leq a$ | $\theta \mapsto | \theta |
| $x \leq 0$ | $\theta \mapsto-\log \left(1+e^{\theta}\right)$ | $\log (\eta)$ |
| $\mathbf{X}^{\top} \mathbf{X}=\mathbf{I}$ | $\boldsymbol{\Theta} \mapsto e^{\text {in }(\boldsymbol{\Theta})-\text { in }(\boldsymbol{\Theta})^{\top}}$ | $\mathbf{U}$ |
Table 1: The parametrisation of the effects. tri(X) is the upper triangular part of the matrix X. For details on the bounds, please refer to the code repository.
Training DiffVox on Professional Vocal Recordings
Building a Diverse Dataset
The researchers trained DiffVox on two datasets: MedleyDB with 70 tracks and an Internal dataset with 365 tracks. Both datasets contain professionally mixed vocal recordings sampled at 44.1 kHz. The training process involved matching the model's output to these professionally processed vocals by adjusting effect parameters through gradient descent.
Optimizing Through Differentiable Loss Functions
Two loss functions guide the optimization process:
Multi-Resolution STFT (MRS) Loss: Minimizes spectral differences between the predicted and target signals across different frequency resolutions.
Multi-Resolution Loudness Dynamic Range (MLDR) Loss: A novel loss function that matches the dynamic characteristics of the signals, particularly useful for optimizing compressor settings.
This dual approach ensures the model captures both spectral and dynamic aspects of vocal processing, which is essential for accurate audio separation tasks.
Efficient Parameter Estimation
The training process normalizes input and target vocals to -18 dB LUFS, splits tracks into twelve-second segments with overlap, and runs for 2,000 steps using the Adam optimizer. The model initializes with neutral settings close to an identity function, then gradually learns optimal parameters. Training each track takes 20-40 minutes on an RTX 3090 GPU, significantly faster than previous approaches thanks to the parallelized differentiable implementations.
Evaluating DiffVox's Performance and Parameter Distributions
Sound Matching Performance
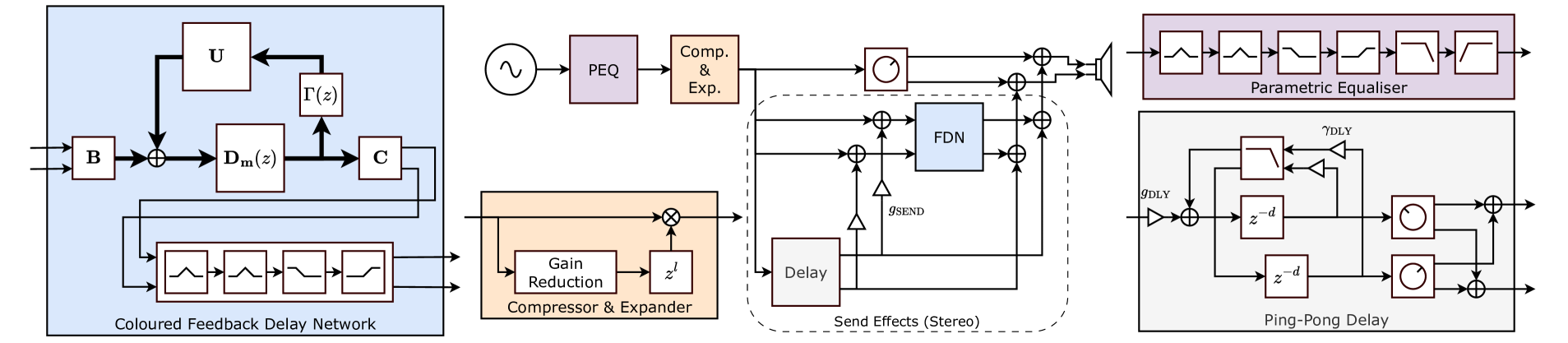
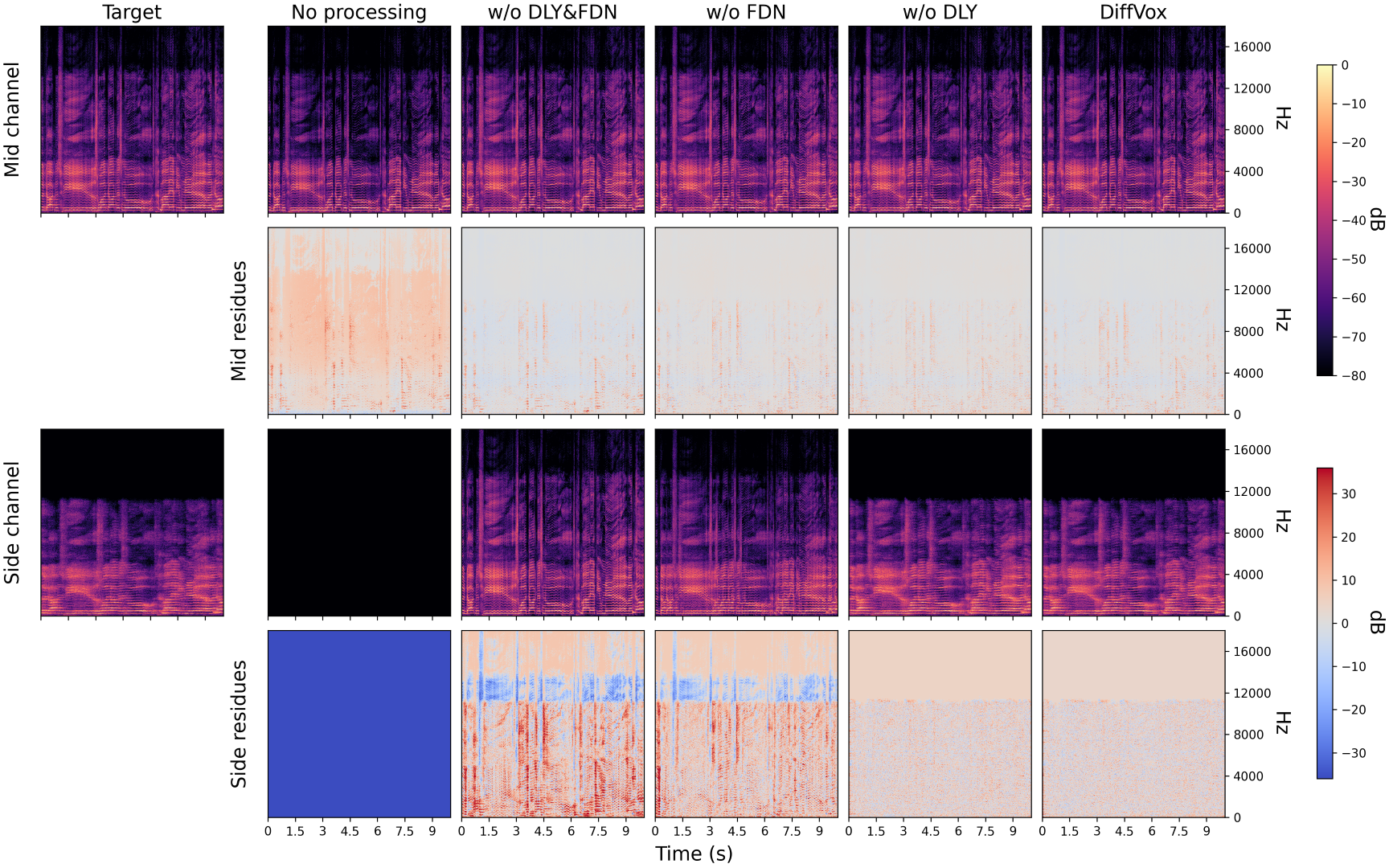
DiffVox achieves impressive matching performance, particularly when including spatial effects. The evaluation metrics show that while the parametric equalizer and compressor match spectral content reasonably well, adding delay and reverb significantly improves the matching of microdynamics.
| Dataset | Configuration | MRS $\downarrow$ | MLDR $\downarrow$ | ||
|---|---|---|---|---|---|
| $\mathrm{l} / \mathrm{r}$ | $\mathrm{m} / \mathrm{s}$ | $\mathrm{l} / \mathrm{r}$ | $\mathrm{m} / \mathrm{s}$ | ||
| Internal | No processing | 1.44 | 2.39 | 1.82 | 2.08 |
| DiffVox | 0.76 | 0.94 | 0.34 | 0.41 | |
| $\vdash$ w/o Approx. | 0.78 | 0.95 | 0.38 | 0.44 | |
| MedleyDB | No processing | 1.27 | 2.16 | 1.00 | 1.35 |
| DiffVox | 0.75 | 0.98 | 0.39 | 0.45 | |
| $\vdash$ w/o Approx. | 0.77 | 1.00 | 0.42 | 0.48 | |
| w/o FDN | 0.79 | 1.14 | 0.48 | 0.62 | |
| w/o DLY | 0.76 | 0.99 | 0.40 | 0.47 | |
| w/o DLY&FDN | 0.61 | 0.90 | 0.82 | 1.17 |
Table 2: Matching performance with different configurations, showing the importance of spatial effects for accurate vocal modeling.
The spectrograms below demonstrate DiffVox's ability to match professional vocal processing across different songs:
Spectrograms comparing different effect configurations when matching the song Torres_NewSkin from MedleyDB.
Spectrograms comparing different effect configurations when matching the song MusicDelta_Country1 from MedleyDB.
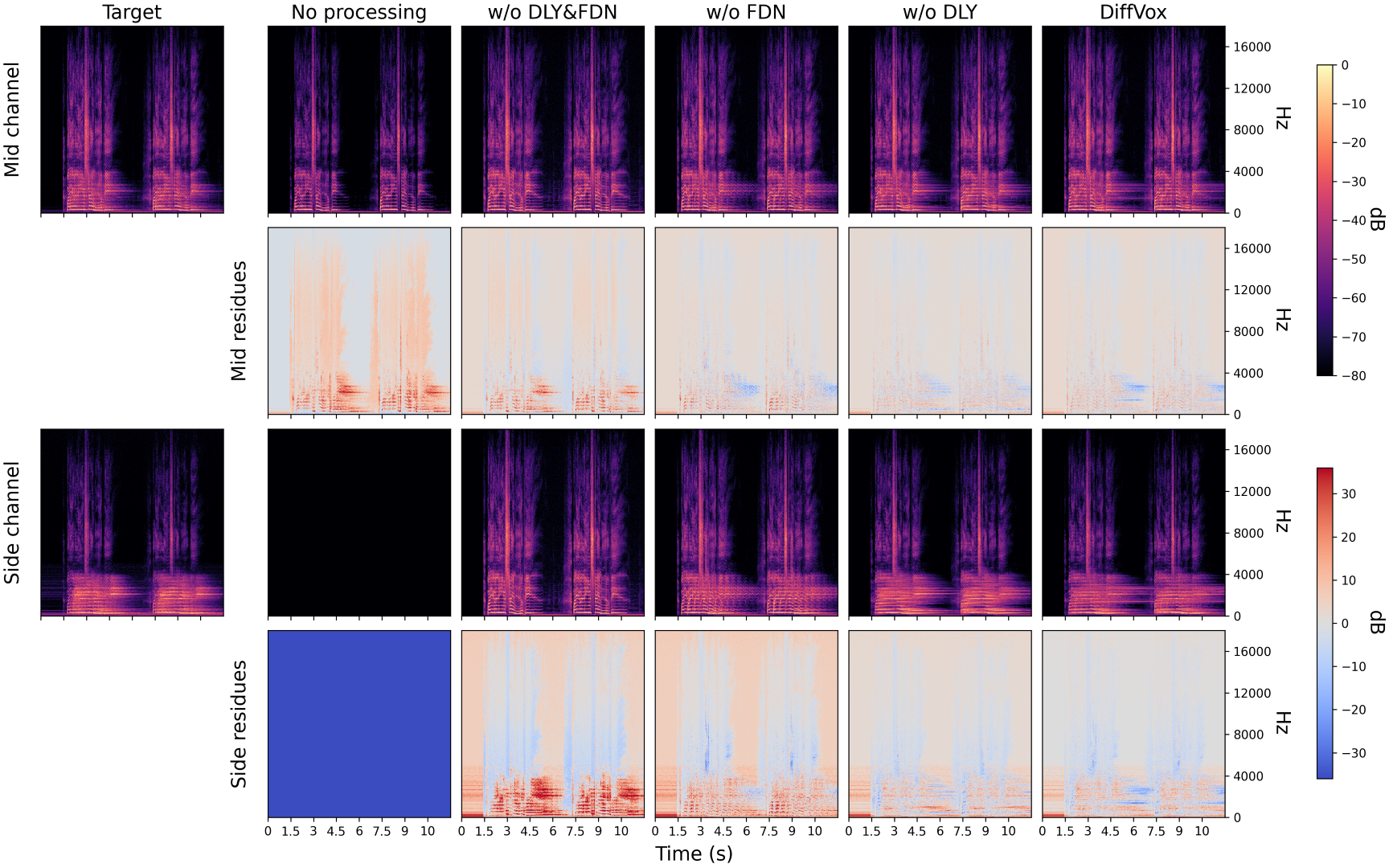
Spectrograms comparing different effect configurations when matching the song StrandOfOaks_Spacestation from MedleyDB.
Parameter Correlation Analysis
The analysis reveals meaningful relationships between effect parameters. Some key findings include:
- Negative correlations between delay time and feedback/delay gain (-0.58/-0.51), indicating that longer delay times are typically used with reduced effect intensity
- Positive correlation between delay feedback gain and low-pass filter cutoff (0.49), showing that darker delays tend to fade out faster
- Strong negative correlation between compressor threshold and make-up gain (-0.55), reflecting the standard practice of increasing make-up gain as threshold decreases
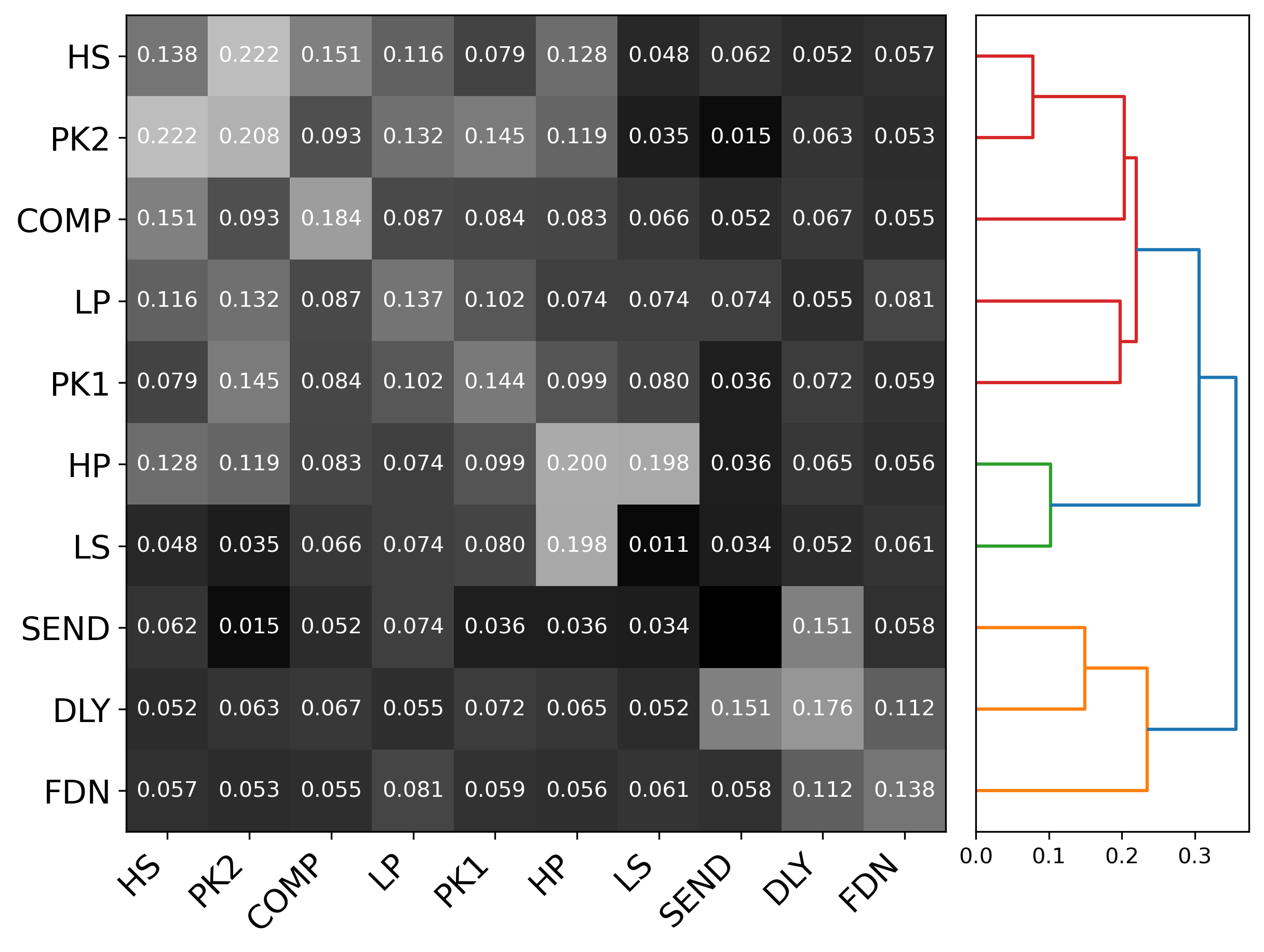
Left: Correlation matrix showing relationships between effect parameters. Right: Hierarchical clustering of effects based on parameter correlations.
| Parameter 1 | Parameter 2 | SCC | |
|---|---|---|---|
| Internal | MedleyDB | ||
| $f_{\mathrm{LP}}$ | $\gamma\left(e^{\sqrt{\frac{10}{10} \pi}}\right)$ | 0.60 | 0.32 |
| $g_{\text {PK2 }}$ | $Q_{\text {PK2 }}$ | $-0.60$ | $-0.10$ |
| $d$ | $\gamma_{\text {DLY }}$ | $-0.58$ | $-0.20$ |
| $f_{\mathrm{LP}}$ | $\gamma\left(e^{\sqrt{\frac{10}{10} \pi}}\right)$ | 0.56 | 0.35 |
| $C T$ | make-up | $-0.55$ | 0.06 |
| $f_{\mathrm{LP}}$ | $\gamma\left(e^{\sqrt{\frac{10}{10} \pi}}\right)$ | 0.53 | 0.19 |
| $E T$ | $E R$ | $-0.52$ | $-0.30$ |
| $d$ | $g_{\text {DLY }}$ | $-0.51$ | $-0.02$ |
| $\gamma_{\text {DLY }}$ | $f_{\text {DLY.LP }}$ | 0.49 | 0.41 |
| $g_{\text {PDN.PK2 }}$ | $f_{\text {PDN.PK2 }}$ | $-0.46$ | $-0.47$ |
Table 3: The top ten most correlated parameters of Internal and their corresponding SCC from MedleyDB.
Hierarchical clustering of the effect parameters revealed three main clusters: spatial effects, low-end shaping filters (HP and LS), and other filters with dynamic processors. This provides insight into how effects naturally group together in professional vocal processing.
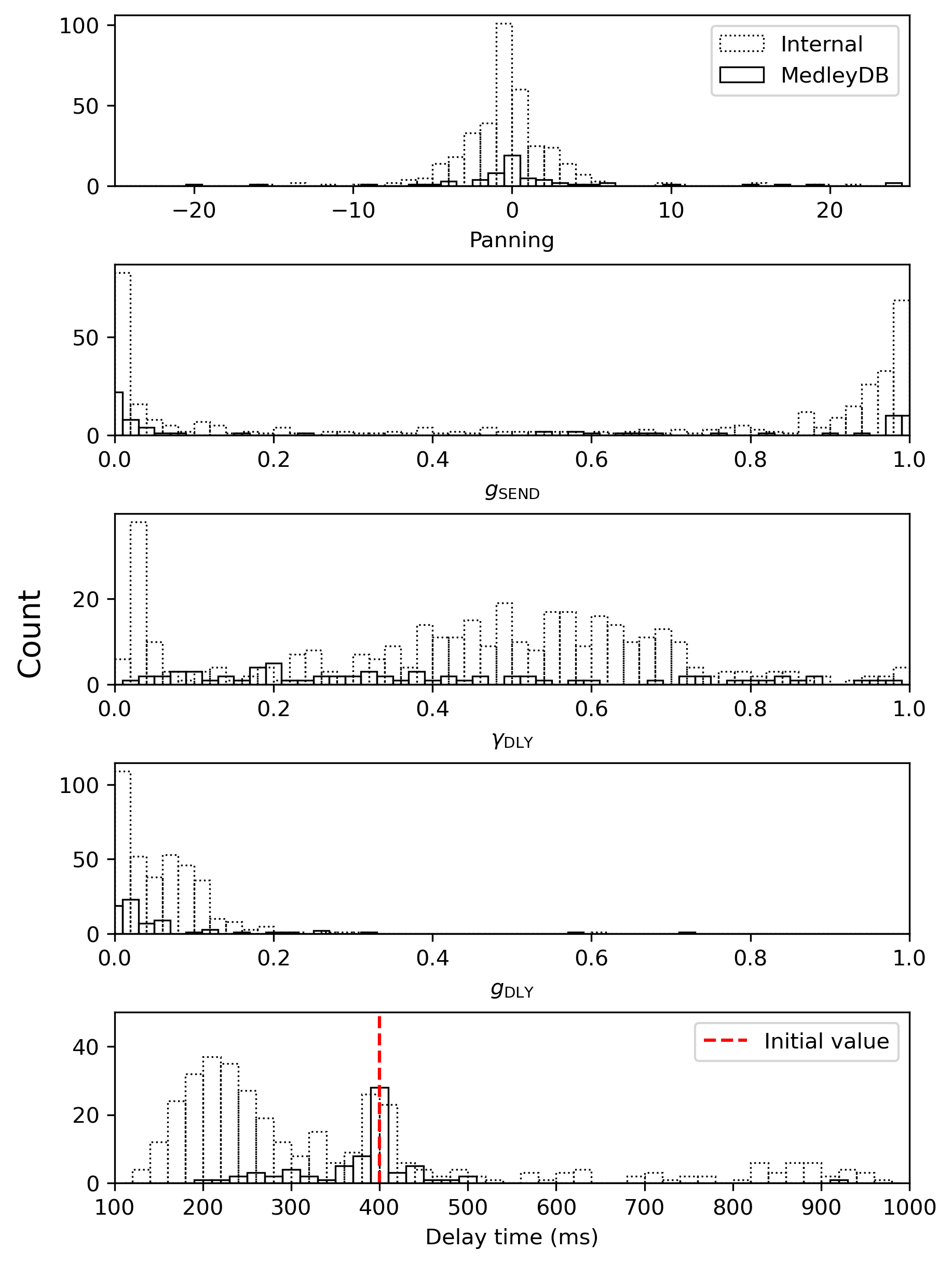
Histograms showing the distribution of panning, delay send, and delay parameters across the analyzed vocal tracks.
Principal Component Analysis
Principal Component Analysis (PCA) reveals the main dimensions of variation in vocal processing. The first principal component primarily controls perceived spaciousness, while secondary components influence spectral brightness.
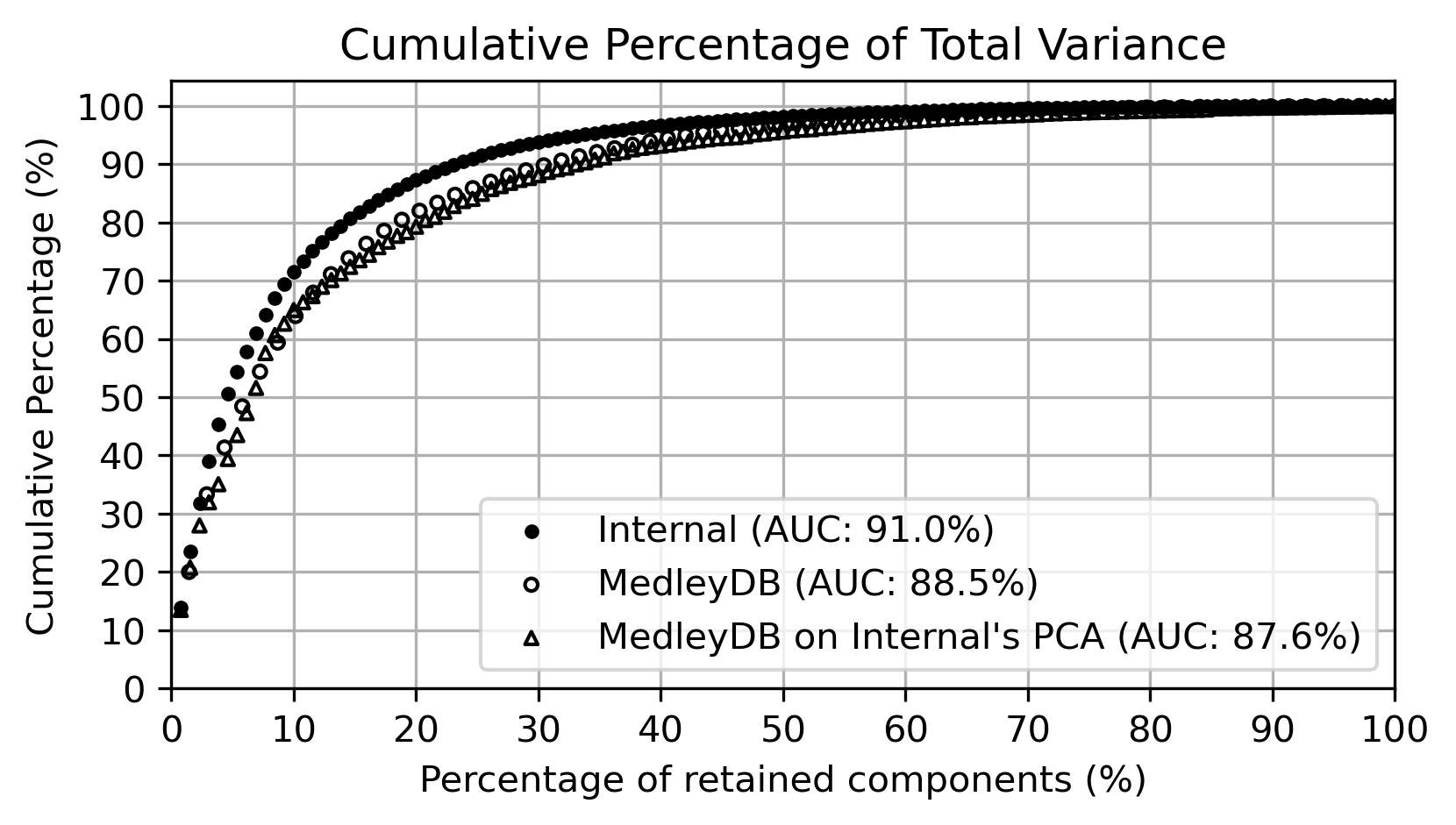
Cumulative total variance as a function of the percentage of retained Principal Components from both PCA models.
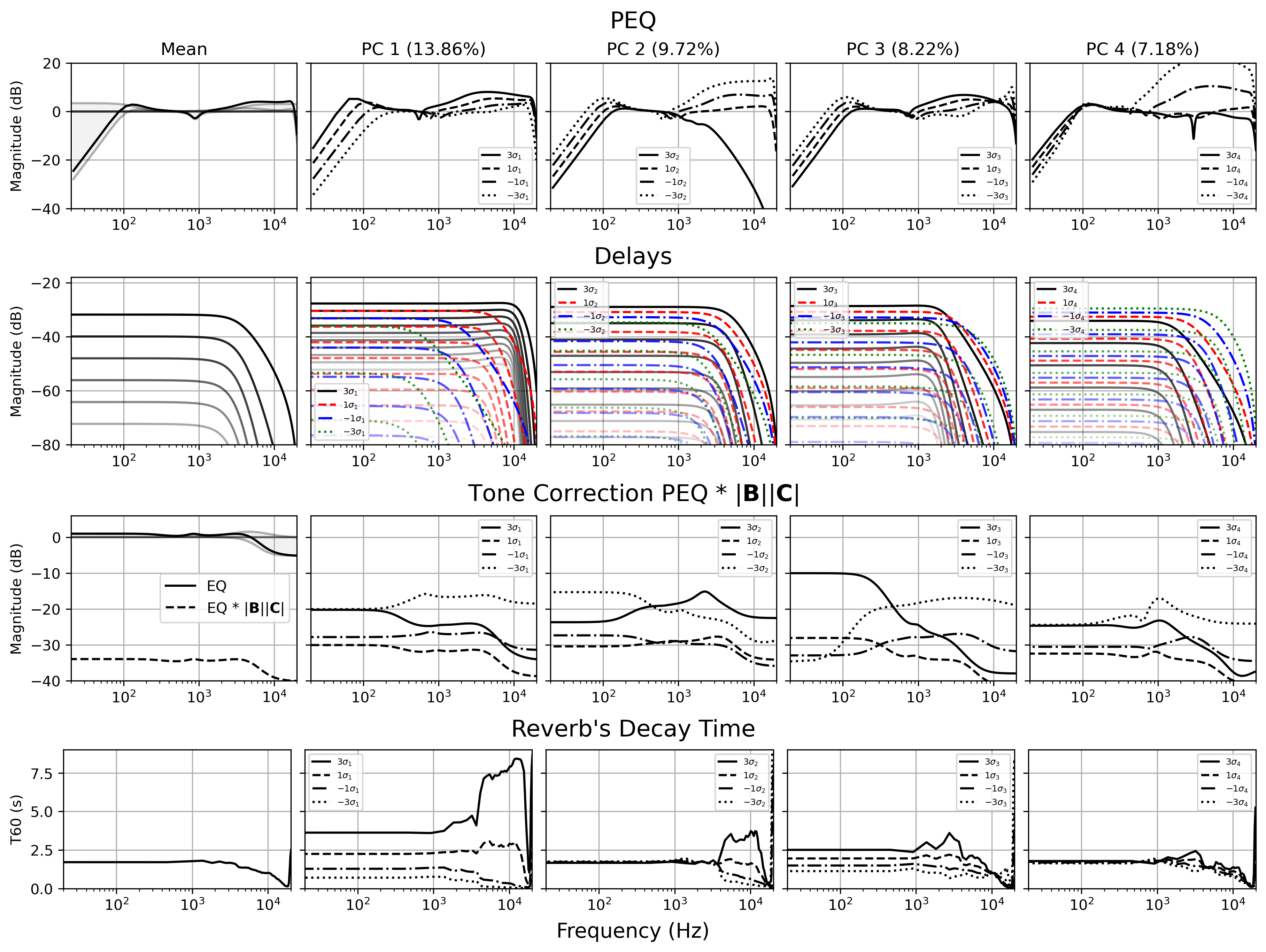
The mean (column one) and the first four principal components of the Internal dataset, showing frequency responses and decay characteristics.
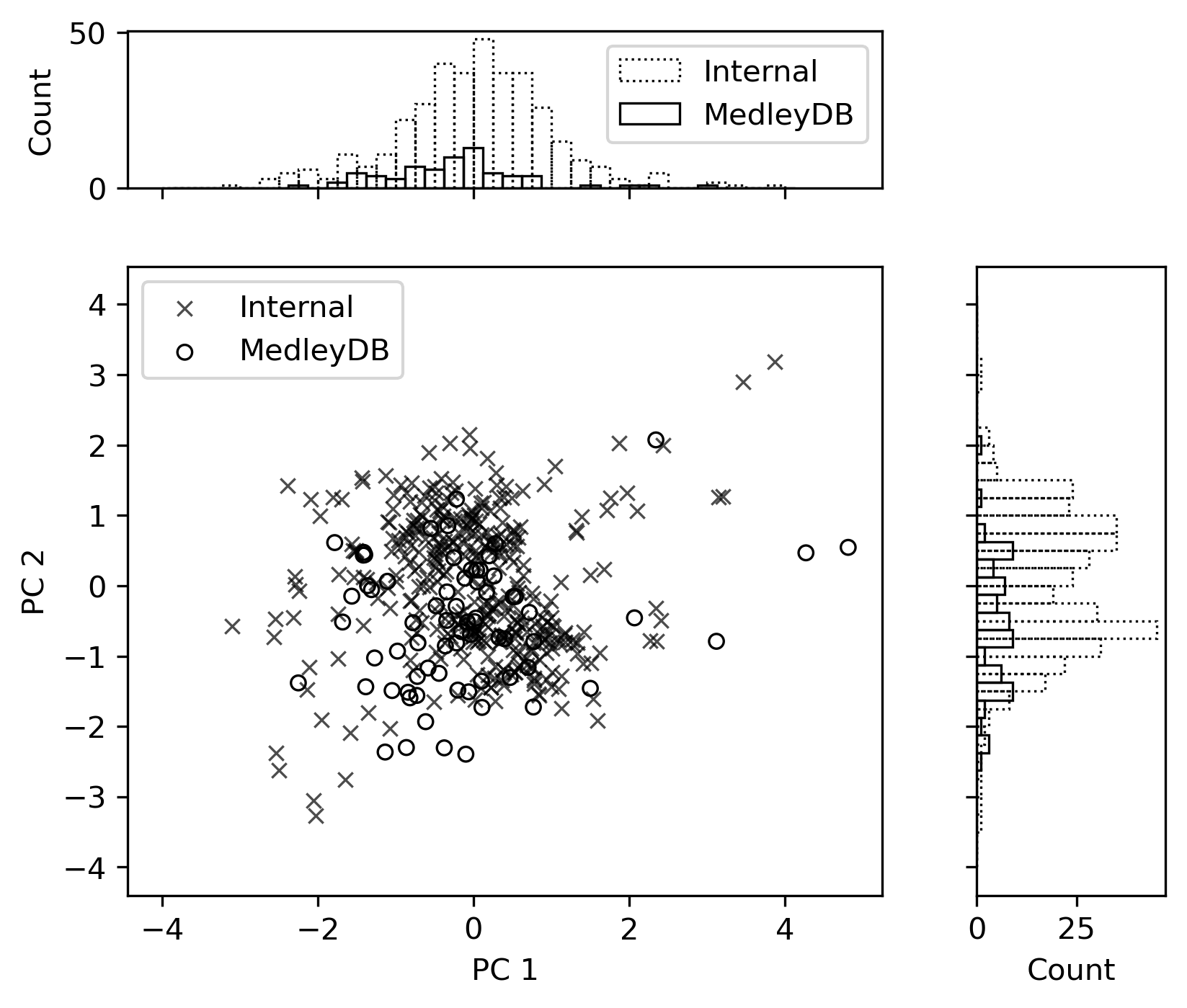
Scatter plot of the first two Principal Components' weights, showing the distribution of vocal processing styles.

Compression curves showing how the mean and principal components affect dynamic processing.
The PCA reveals connections to McAdams' timbre dimensions, with the most important component controlling perceived spaciousness while secondary components influence spectral brightness. Statistical testing confirms the non-Gaussian nature of the parameter distribution, highlighting the complexity of vocal effects configurations.
Conclusions and Future Directions
DiffVox demonstrates that spatial effects are essential for accurately matching professional vocal processing. The model reveals meaningful correlations between effect parameters that reflect common practices in music production, such as the collaborative use of high-pass and low-shelf filters to shape the low end.
The non-Gaussian distribution of parameters suggests that more sophisticated generative models will be needed to fully capture the complexity of vocal effects. The researchers have released their dataset of 435 vocal presets along with the DiffVox model implementation to foster further research.
This work provides valuable insights for developing more realistic automatic mixing tools and neural audio effect models. Future research could extend the approach to multi-track scenarios and explore more sophisticated generative models for capturing the true distribution of professional audio effects parameters.