This is a Plain English Papers summary of a research paper called Better Glass: Extended PBR Materials for Realistic Image Synthesis. If you like these kinds of analysis, you should join AImodels.fyi or follow us on Twitter.
The Challenge of Realistic Transparent Materials in Image Synthesis
Realistic image synthesis faces a fundamental challenge: accurately rendering complex materials, especially surfaces with high specularity and transparency. Current approaches stand at opposite ends of a spectrum - physically based rendering (PBR) offers high realism but demands significant computational resources, while learning-based methods provide efficiency but often lack physical consistency.
The gap becomes particularly evident when dealing with glass, mirrors, and polished metals - materials common in indoor environments but poorly handled by traditional PBR materials. These materials involve both reflection and transmission properties that standard models struggle to represent faithfully.
The ePBR: Extended PBR Materials research introduces a solution: extending intrinsic image representation to incorporate both reflection and transmission properties. This approach enables more accurate synthesis of transparent materials while maintaining the efficiency needed for practical applications.

Examples of highly specular and transparent objects commonly found in real-world environments.
The researchers propose an explicit intrinsic compositing framework that delivers deterministic, interpretable image synthesis with precise material controls. Unlike diffusion-based approaches like those found in Collaborative Control: Geometry-Conditioned PBR Image Generation, this method provides accurate control over high-specular regions while requiring minimal computational resources.
The Current Landscape: Understanding PBR and Image Synthesis Approaches
Physically Based Rendering
PBR has been a cornerstone of computer graphics, simulating how light interacts with complex scene elements including geometry, materials, and illumination. Traditional rendering pipelines rely on Monte Carlo light transport simulation, which despite its accuracy, introduces noise due to limited sampling.
A key challenge in PBR is material representation. Real-world surfaces are modeled by the Bidirectional Scattering Distribution Function (BSDF). The Disney Principled BSDF has become particularly influential, balancing physical principles with artistic control. This approach has shaped material systems across platforms including Blender, Unreal Engine, and Mitsuba3.
However, real-world materials are far more complex than simple surface models. Specific materials like layered objects, hair, cloth, and iridescent surfaces require specialized appearance models to achieve realism. This complexity is also addressed in specialized applications like EndoPBR: Material and Lighting Estimation for Photorealistic Surgical Simulations.
Data-driven Image Synthesis
Recent advances in image synthesis have moved toward generative models that diverge from classical rendering methodologies. Large-scale diffusion models like DALL·E and Stable Diffusion have shown remarkable success in producing realistic images by iteratively refining noise into structured visual content. Unlike traditional PBR, these approaches learn complex visual distributions from extensive datasets, synthesizing diverse imagery without explicit physical simulation.
The trade-off is that these models are difficult to train and generate images that are hard to control precisely. Various approaches attempt to address this limitation through fine-tuning pre-trained models. ControlNet has gained wide adoption for tasks requiring precise layout control, while approaches like IC-Light focus on manipulating illumination while preserving image details.
Intrinsic Representation
Intrinsic representation offers a promising middle ground between physically-based rendering and generative models. By decomposing a scene into fundamental components like geometry, materials, and illumination, this approach enables structured yet editable scene manipulation that maintains a connection to physical properties.
These representations have been integrated into neural rendering and inverse graphics frameworks, facilitating explicit control over scene components. Various types of intrinsic representations focus on different aspects:
- Geometry representations recover structural scene information like normal and depth maps
- Lighting representations estimate scene illumination separately from geometry and reflectance
- Reflectance-shading separates images into reflectance (albedo) and shading components
The most common representation in recent research uses parametric microfacet BRDF with PBR materials. This approach has expanded from single object tasks to complex indoor image decomposition and editing, as also explored in IntrinsiX: High Quality PBR Generation using Image Decomposition.
Transparent/Translucent Material
Most current image manipulation techniques only account for diffuse and specular reflectance, neglecting transparent materials that include both light reflection and transmission (BTDF). Only a few works consider glass-like materials:
- Materialist supports adding transparent objects but treats them as a special case
- The Alchemist can control transparency of a single object using a learning approach
- Some SVBRDF research incorporates transparency as an intrinsic map for fabrics
This gap in handling transparent materials motivates the development of ePBR materials.
Extending PBR: The ePBR Material Model
Building on the Rendering Equation
The rendering equation for a non-emissive surface point forms the foundation of the ePBR approach. This equation calculates outgoing radiance as an integration of incident light from all directions, weighted by the BSDF at that point.
The Disney Principled BSDF has gained wide adoption in rendering engines due to its versatility in handling various materials and lighting effects. However, most research implements a simplified version that only represents a surface's diffuse and specular reflection.
The ePBR model extends this approach to a thin-surface model that handles both reflection and transmission:
f = kd·fd + ks·fs + kt·ft
Where:
- kd, ks, and kt are coefficients for diffuse, specular reflectance, and specular transmittance terms
- fd, fs, and ft represent the associated functions for each component
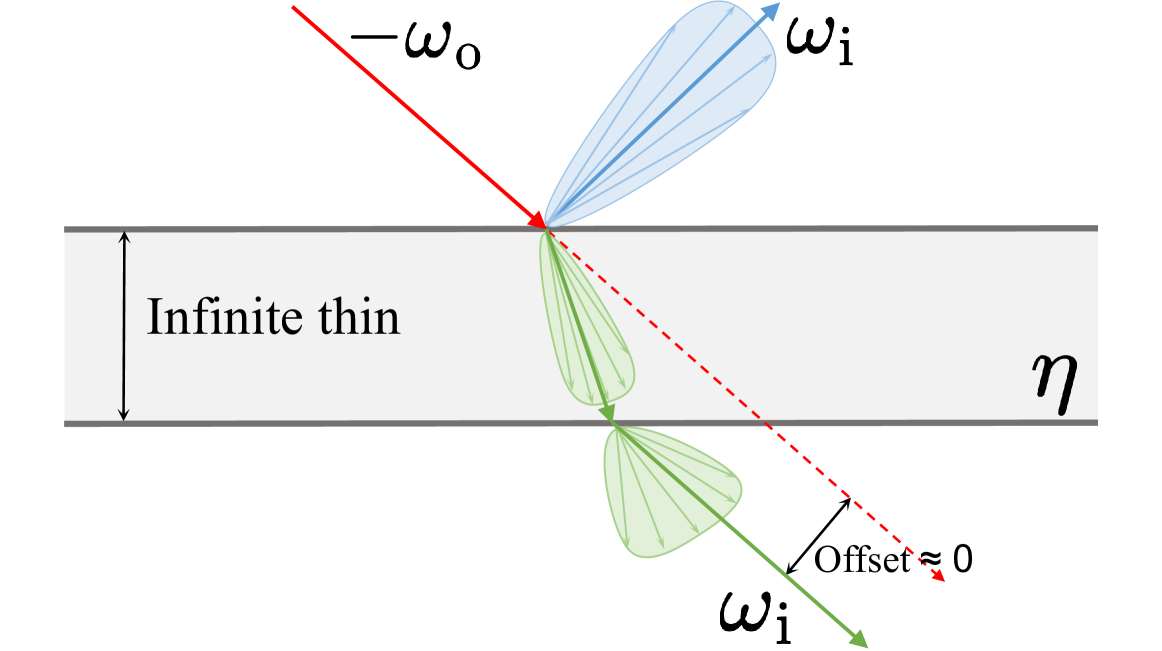
Thin surface assumption used in the ePBR model. Light refraction occurs twice (entering and exiting) while reflection happens once on the top surface.
Handling Reflection in ePBR
The diffuse component uses the Lambertian model to estimate diffuse reflectance, where albedo (a) represents the inherent color of the surface:
fd = a/π
For specular reflectance, the research employs a microfacet model without considering clearcoat:
fs = D(hr)·F(hr,ωo)·G(hr,ωo,ωi) / (4|ωo·n|·|ωi·n|)
This equation incorporates:
- Normal distribution function (D) using GGX distribution
- Fresnel reflection coefficient (F) using Schlick's approximation
- Geometric attenuation (G) using Smith's method with Schlick approximation
These components work together to model how light interacts with microscopically rough surfaces.
Adding Transparency: The Thin Surface Model
The research focuses on thin surfaces with two parallel surfaces and zero thickness - an approximation of transparent surfaces like windows or glass tables. This simplification allows for a more tractable model compared to modeling general transparent objects like bottles.
With this thin surface assumption, light bending due to refraction approximately cancels out, and the offset between incoming and outgoing light can be ignored. The specular transmission is modeled similarly to the specular reflection term but reflected to the other side:
ft = D̂(ht)·F(ht,ωo)·G(ht,ωo,ωi) / (4|ωo·n|·|ωi·n|)
The key differences are:
- Extended Normal Distribution Function (D̂) estimated by joint spherical warping
- A different half vector calculation that accounts for transmission
Putting It All Together: The Complete ePBR Model
The final ePBR material model combines the three terms:
f = (1-t)(1-m)fd + fs + t·ft
Where:
- m is metallic
- t is transparency
- Albedo (a) is shared with the incident specular response for metallic materials
This model can represent several special cases through parameter combinations:

Visual comparison of three typical materials represented by the ePBR model: metal, dielectric, and glass.
- When t=0, m=0: Standard dielectric materials (diffuse + specular)
- When t=0, m=1: Conductor/metal (specular only with albedo as Fresnel term)
- When t=1, m=0: Transparent glass (specular reflection + transmission)
The model automatically sets m=0 when t>0 to avoid invalid materials like transparent metal. This approach to material generation complements other research like MaterialMVP: Illumination-Invariant Material Generation.
From Theory to Practice: Screen-space Image Synthesis with ePBR
The practical implementation uses intrinsic channels in screen space to synthesize the final image. The rendering equation is split into three components for implementation, with each component handled separately.
Computing Diffuse Reflectance
For the diffuse component, calculation is straightforward:
Md = ∫(a/π)·|ωi·n|·dωi = a
The corresponding diffuse irradiance (Ed) represents the amount of light reaching a shading point integrated over the cosine-weighted hemisphere. This can be directly estimated from the input image.
The diffuse reflectance is then:
Idiff = A·E
Where A is the albedo map in screen space and E is the diffuse irradiance map.
Handling Specular Reflectance
For the specular component, the model converts the term into a linear function of F0:
Ms = ∫fs(ωo,ωi)·|ωi·n|·dωi = A·F0 + B
The values A and B depend on roughness (R) and can be precomputed in a lookup table.
Instead of using importance sampling to convolve the environment map with the GGX distribution, the approach defines a normalized filtering kernel based on D(h)·|ωi·n|. This creates blurring effects when applied to a mirror-like reflection image:

Comparison of roughness rendering between the proposed filtering method and ground truth path tracing with Monte Carlo sampling.
To obtain the reflection layer, the method uses Screen Space Ray Tracer (SSRT) to find the reflection color for each pixel:

Process of generating mirror reflectance image using Screen Space Ray Tracing (SSRT).
The final specular reflectance is calculated as:
Ispec = (A·F0+B)·Conv(K,Amr)
Implementing Specular Transmittance
The transmittance calculation follows a similar approach to specular reflectance. The key difference is that the kernel applied to the background image has a wider distribution since light passes through both the top and bottom surfaces.
Assuming both surfaces have the same roughness, the method simply applies the kernel twice:
Et = Conv(K,Conv(K,Abg))
The specular transmittance is then:
Itran = (A·F0+B)·Conv(K,Conv(K,Abg))·A
Finally, the three layers are combined to create the final image:
I = (1-T)(1-M)·Idiff + Ispec + T·Itran
Seeing is Believing: Results and Evaluation
Understanding ePBR Material Representation
The ePBR model uses various intrinsic channels, each with specific physical meaning and representation:
| $\mathbf{X}$ | Type | Range | Description | |
|---|---|---|---|---|
| N | $\mathbb{R}^{H \times W \times 3}$ | $[-1,1]$ | Normal | |
| D | $\mathbb{R}^{H \times W}$ | $[0,1]$ | Depth | |
| A | $\mathbb{R}^{H \times W \times 3}$ | $[0,1]$ | Albedo | |
| R | $\mathbb{R}^{H \times W}$ | $[0,1]$ | Roughness | |
| M | $\mathbb{R}^{H \times W}$ | $[0,1]$ | Metallic | |
| T | $\mathbb{R}^{H \times W}$ | $[0,1]$ | Transparency | |
| E | $\mathbb{R}^{H \times W \times 3}$ | $[0, \infty)$ | Diffuse irradiance | |
| $\mathbf{A}_{\mathrm{mr}}$ | $\mathbb{R}^{H \times W \times 3}$ | $[0, \infty)$ | Mirror reflectance | |
| $\mathbf{A}_{\mathrm{bg}}$ | $\mathbb{R}^{H \times W \times 3}$ | $[0, \infty)$ | Background radiance |
The intrinsic channels used in the ePBR model, including geometry, materials, and illumination components.
Each channel must have the same resolution as the final image, possess unique physical meaning for precise editing, and have uniformly distributed values. Notably, the transparency map (T) is stored in the blue channel of the material map without requiring additional memory.
How Material Properties Affect Appearance
The research demonstrates how changing intrinsic material properties affects the final rendered appearance:

Visual evaluation of how different material parameters in the ePBR model affect the rendered appearance.
- Metallic: As metallicity increases, the diffuse layer gradually disappears and highlights shift from light to metal color
- Roughness: Controls the blurring of both reflection and transmission
- Transparency: Determines how much light passes through the surface and how clearly the background is visible
- Albedo: Represents nonabsorbed light, affecting color and transparency effectiveness
Comparing Image Composition Methods
The research validates that the proposed image composition method produces more faithful results compared to diffusion-based methods like RGB↔X. Using test examples from the InteriorVerse dataset, the method demonstrates better handling of high-specular regions such as floors, windows, and glass decorations.
| LPIPS $\downarrow$ | |||||
|---|---|---|---|---|---|
| Fig. 7(a) | (b) | (c) | (d) | (e) | |
| $\mathrm{RGB} \leftrightarrow \mathrm{X}$ | 0.493 | 0.360 | 0.372 | 0.387 | 0.327 |
| Ours | $\mathbf{0 . 4 1 4}$ | $\mathbf{0 . 2 7 1}$ | $\mathbf{0 . 3 6 0}$ | $\mathbf{0 . 3 3 6}$ | $\mathbf{0 . 3 0 4}$ |
LPIPS error metrics comparing the proposed method with diffusion-based RGB↔X. Lower values indicate better performance.
LPIPS error metrics confirm the reliability of the composition method, showing particular improvement in mirror-like areas. This performance aligns with other image decomposition approaches like IntrinsiX: High Quality PBR Generation using Image Decomposition.
Limitations and Future Directions
The ePBR material model represents a simplified approach that doesn't consider anisotropic effects or subsurface scattering. For transparent objects, only thin surfaces are supported - accurate refraction through thick objects would require geometry knowledge of the backside, which is difficult to estimate from screen space information.
The image composition method is straightforward but cannot handle multiple reflections or color bleeding. The final image quality depends entirely on the accuracy of the intrinsic channels.
Despite these limitations, the research suggests that datasets generated with ePBR materials could enhance learning-based methods for image decomposition, synthesis, and texture generation.
The Promise of Extended PBR Materials
The ePBR approach successfully extends intrinsic representations to incorporate both reflection and transmission properties, enabling more accurate synthesis of transparent materials like glass and windows. The explicit intrinsic compositing framework delivers deterministic and interpretable image synthesis with precise control over material properties.
Compared to diffusion-based rendering methods, this approach provides an efficient and memory-friendly solution suitable for real-time applications and high-resolution image generation. The flexible material editing maintains physical plausibility while offering intuitive control.
Future work will focus on integrating ePBR materials into more 3D vision applications to bridge the gap between physically-based and AI-driven image synthesis. This research has potential to impact downstream applications by improving control over low-level object properties across various domains.

