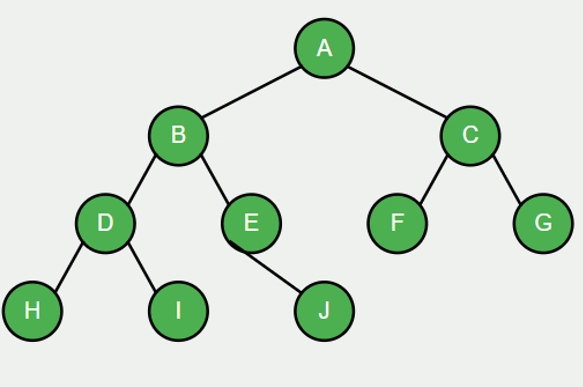
Tree Structure
Each node x has these attributes:
-
x.key: key stored in the node -
x.p: pointer to the parent node -
x.left: pointer to the left child -
x.right: pointer to the right child
A tree T has:
-
T.root: pointer to the root node
Algorithms
1. Inorder Tree Walk
Input: x (pointer to a node in the binary search tree)
Output: None (prints keys in order)
1. If x ≠ null
2. Inorder-tree-walk(x.left)
3. Print x.key
4. Inorder-tree-walk(x.right)2. Tree Search (Recursive)
Input: x (pointer to subtree root), k (key to search)
Output: Pointer to node with key k (or null if not found)
1. If x == null or k == x.key
2. Return x
3. If k < x.key
4. Return tree-search(x.left, k)
5. Else
6. Return tree-search(x.right, k)3. Iterative Tree Search
Input: x (pointer to subtree root), k (key to search)
Output: Pointer to node with key k (or null if not found)
1. While x ≠ null and k ≠ x.key
2. If k < x.key
3. x = x.left
4. Else
5. x = x.right
6. Return x4. Tree Minimum
Input: x (pointer to non-null node)
Output: Pointer to node with minimum key in the subtree
1. While x.left ≠ null
2. x = x.left
3. Return x5. Tree Maximum
Input: x (pointer to non-null node)
Output: Pointer to node with maximum key in the subtree
1. While x.right ≠ null
2. x = x.right
3. Return x6. Tree Insert
Input: t (binary search tree), z (node to insert)
Output: None (modifies tree by inserting z)
1. y = null
2. x = t.root
3. While x ≠ null
4. y = x
5. If z.key < x.key
6. x = x.left
7. Else
8. x = x.right
9. z.p = y
10. If y == null
11. t.root = z
12. Elseif z.key < y.key
13. y.left = z
14. Else
15. y.right = z7. Transplant (Helper for Delete)
Input: t (binary search tree), u (subtree to replace), v (replacing subtree)
Output: None (modifies tree)
1. If u.p == null
2. t.root = v
3. Elseif u == u.p.left
4. u.p.left = v
5. Else
6. u.p.right = v
7. If v ≠ null
8. v.p = u.p8. Tree Delete
Input: t (binary search tree), z (node to delete)
Output: None (modifies tree)
1. If z.left == null
2. Transplant(t, z, z.right)
3. Elseif z.right == null
4. Transplant(t, z, z.left)
5. Else
6. y = tree-minimum(z.right)
7. If y.p ≠ z
8. Transplant(t, y, y.right)
9. y.right = z.right
10. y.right.p = y
11. Transplant(t, z, y)
12. y.left = z.left
13. y.left.p = yAdditional Tree Operations
Size
Input: T (binary tree)
Output: Number of nodes in the tree
1. If T.root == Null
2. Return 0
3. count = 0
4. sizeHelper(T.root, count)
5. Return countOther Basic Operations
-
isEmpty(): Returns true if tree is empty -
root(): Returns the root node -
parent(v): Returns parent of node v -
children(v): Returns list of children of node v -
leftChild(v): Returns left child of node v -
rightChild(v): Returns right child of node v -
sibling(v): Returns sibling of node v
Traversal Algorithms
Preorder Traversal
Input: v (node)
Output: None
1. If v == Null
2. Return
3. Visit v
4. If isInternal(v)
5. preorder(v.left)
6. preorder(v.right)Postorder Traversal
Input: v (node)
Output: None
1. If v == Null
2. Return
3. If isInternal(v)
4. postorder(v.left)
5. postorder(v.right)
6. Visit vInorder Traversal
Input: v (node)
Output: None
1. If v == Null
2. Return
3. If v.left ≠ Null
4. inorder(v.left)
5. Visit v
6. If v.right ≠ Null
7. inorder(v.right)Euler Tour Traversal
Input: v (node)
Output: None
1. If v == null
2. Return
3. visitBeforeSubtrees(v)
4. If isInternal(v)
5. If v.left ≠ Null
6. eulerTour(v.left)
7. visitBetweenSubtrees(v)
8. If v.right ≠ Null
9. eulerTour(v.right)
10. visitAfterSubtrees(v)Time Complexity Summary
| Operation | Time Complexity |
|---|---|
| Inorder Walk | O(n) |
| Tree Search | O(h) |
| Tree Insert | O(h) |
| Tree Delete | O(h) |
| Size | O(n) |
| Traversals | O(n) |
Note: h = height of the tree, n = number of nodes
Euler Tour Example
The Euler Tour captures all tree traversal information in a single walk:
- Each node is visited exactly 3 times
- Combines preorder, inorder, and postorder traversals
Example Tree Expression
The Euler Tour can help evaluate complex tree expressions:
((3+1)×(9−5))−(3×(7−4)+6)This demonstrates how Euler Tour can be used to systematically process and evaluate tree-based mathematical expressions.
Binary Search Tree Operations Complexity Table
| Operation | Time Complexity (Big-O) |
|---|---|
| inorder-tree-walk | O(n) |
| tree-search | O(h) |
| iterative-tree-search | O(h) |
| tree-minimum | O(h) |
| tree-maximum | O(h) |
| tree-insert | O(h) |
| tree-delete | O(h) |
| transplant | O(1) |
| size | O(n) |
| isEmpty | O(1) |
| root | O(1) |
| parent | O(1) |
| children | O(1) |
| leftChild | O(1) |
| rightChild | O(1) |
| sibling | O(1) |
| isInternal | O(1) |
| isExternal | O(1) |
| isRoot | O(1) |
| preorder | O(n) |
| postorder | O(n) |
| inorder | O(n) |
| eulerTour | O(n) |
Euler Tour Example with Larger Tree
Euler Tour traversal sequence for a tree with 3 layers:
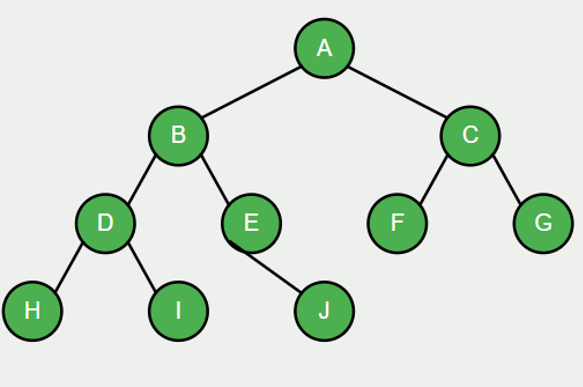
- A (first visit)
- B (first visit)
- D (first visit)
- H (first visit)
- H (second visit) - no children
- H (third visit)
- D (second visit)
- I (first visit)
- I (second visit) - no children
- I (third visit)
- D (third visit)
- B (second visit)
- E (first visit)
- J (first visit)
- J (second visit) - no children
- J (third visit)
- E (second visit) - E has no right child
- E (third visit)
- B (third visit)
- A (second visit)
- C (first visit)
- F (first visit)
- F (second visit) - no children
- F (third visit)
- C (second visit)
- G (first visit)
- G (second visit) - no children
- G (third visit)
- C (third visit)
- A (third visit)
Note: Each node is visited exactly 3 times, creating a complete "tour" around the tree that captures all the information from preorder, inorder, and postorder traversals in a single walk.
Mathematical Expression Using Euler Tour Algorithm
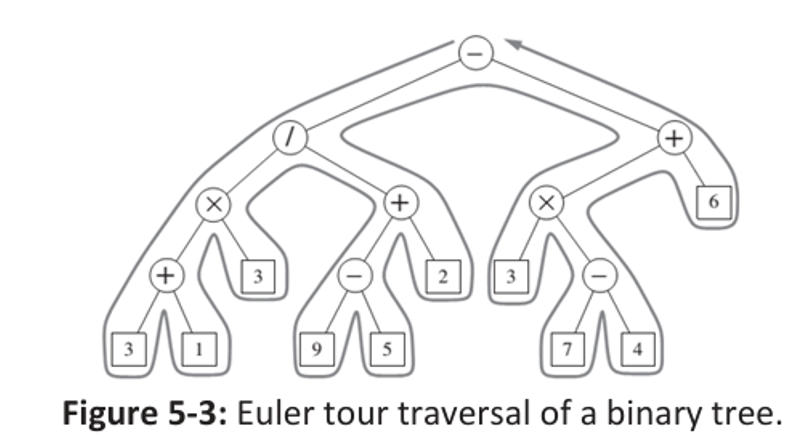
Q: What is the mathematical expression for this tree when using the Euler Tour algorithm?
Solution:
-
Start with the left subtree of the root (-):
- Left subtree of ×: (3 + 1)
- Right subtree of ×: (9 - 5)
- Combine: (3 + 1) × (9 - 5)
-
Move to the right subtree of the root (-):
- Left subtree of +: 3 × (7 - 4)
- Right subtree of +: 6
- Combine: 3 × (7 - 4) + 6
-
Combine the results from the left and right subtrees of the root:
- Left: (3 + 1) × (9 - 5)
- Right: 3 × (7 - 4) + 6
- Combine: ((3 + 1) × (9 - 5)) - (3 × (7 - 4) + 6)
Final Answer:
The mathematical expression represented by the tree is:
((3+1)×(9−5))−(3×(7−4)+6) => ((4)×(4))−(3×(3)+6) = 16 − (3×3 + 6) = 16 − (9 + 6) = 16 − 15 = 1