🔍 Breadth-First Search (BFS) Algorithm

🧠 Imagine This:
You’re in a maze of rooms. You want to find the shortest way out. So you start from the first room, check all the adjacent rooms, then go to the next layer of rooms, and keep expanding until you reach the exit.
That’s Breadth-First Search (BFS) – you explore layer by layer, level by level.

📘 What is BFS?
Breadth-First Search (BFS) is a fundamental graph traversal algorithm that explores nodes level by level. It's particularly useful for finding the shortest path in unweighted graphs.
Think of it like exploring a tree horizontally: you check all your siblings before going to your cousins!

🧠 How It Works
1.Start from a node (say, node 0).
2.Use a queue to remember "what to visit next".
3.Keep a visited[] array so you don’t repeat visits.
4.For every node:
Add its unvisited neighbors to the queue.
Visit them one by one.
📥Queue ensures order — first in, first out. Perfect for level-wise
traversal.

🤝 Use-Cases in Real World
Social Network Suggestions (Who’s 1 friend away from your friend?)
Web Crawling
Shortest Path in Unweighted Graphs
Peer-to-Peer Networks

🔄 Dry Run Example (Graph)

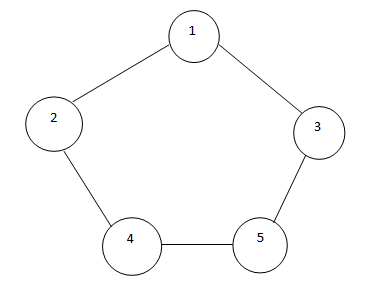
✅ Traversal Order: 1 → 2 → 3 → 4 → 5
✅ Explanation:
Start from node 1 → enqueue neighbors 2 and 3
Visit 2 → enqueue 4
Visit 3 → enqueue 5
Visit 4 (already added)
Visit 5
Queue becomes empty → traversal ends

#include 
#include 
#include 
using namespace std;

vector bfsOfGraph(int V, vector adj[]) {
    vector bfs;
    vector visited(V, false);
    queue q;

    // Start BFS from node 0
    q.push(0);
    visited[0] = true;

    while (!q.empty()) {
        int node = q.front();
        q.pop();
        bfs.push_back(node);

        for (int neighbor : adj[node]) {
            if (!visited[neighbor]) {
                visited[neighbor] = true;
                q.push(neighbor);
            }
        }
    }

    return bfs;
}

int main() {
    int V = 5;
    vector adj[V];

    // Undirected Graph Example
    adj[0] = {1, 2};
    adj[1] = {0, 3};
    adj[2] = {0, 4};
    adj[3] = {1};
    adj[4] = {2};

    vector result = bfsOfGraph(V, adj);

    cout << "BFS Traversal: ";
    for (int node : result)
        cout << node << " ";
    cout << endl;

    return 0;
}

📈 Time & Space Complexity
Time Complexity: O(V + E)
Space Complexity: O(V)
Where V is the number of vertices and E is the number of edges.

🧊 Key Takeaways
BFS is great for finding the shortest path (in unweighted graphs).
It uses a queue to traverse level-by-level.
Ideal when you want to explore everything close to you first.