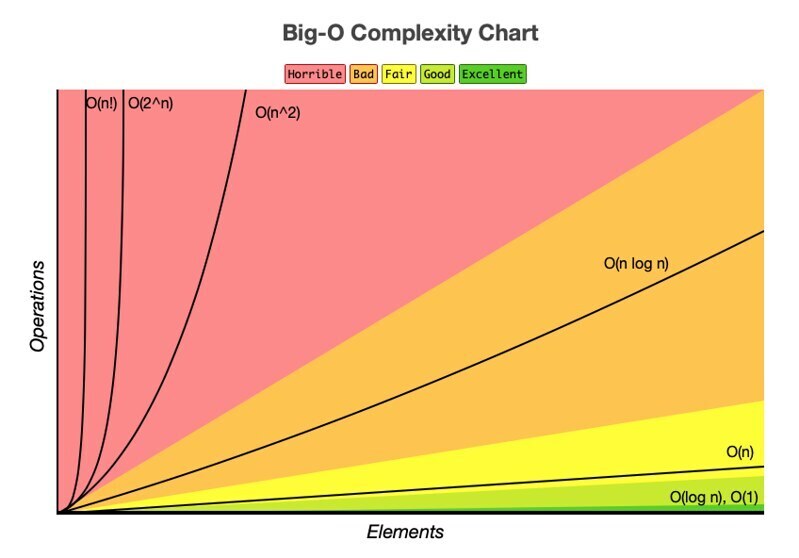
Cuando empiezas a estudiar algoritmos, una de las primeras cosas que te encuentras es la notación Big-O: O(n), O(log n), O(n^2)...
Al inicio puede parecer algo abstracto o complicado, pero con la práctica, será fácil de entender. En este post explicaré qué es la complejidad algorítmica, cómo se calcula.
1. ¿Qué es la complejidad algorítmica?
Es una forma de medir qué tan eficiente es un algoritmo, tanto en tiempo (cuánto tarda) como en espacio (cuánta memoria usa), dependiendo del tamaño de la entrada.
Usamos notaciones como:
- O(1): constante
- O(n): lineal
- O(log n): logarítmica
- O(n^2): cuadrática
- O(2^n): exponencial
No se mide en segundos ni en kilobytes exactos, sino en cómo crece el tiempo/memoria a medida que crece el problema.
2. La famosa "O" y el logaritmo
▶ ¿Qué significa la O en O(n)?
Es una forma de decir "el orden de crecimiento". Nos enfocamos en el peor caso.
▶ ¿Y qué es log(n)?
Es el logaritmo en base 2. Se usa cuando un algoritmo divide en partes, como la búsqueda binaria.
Ejemplo: log₂(16) = 4, porque:
16 → 8 → 4 → 2 → 1 (4 pasos)
3. Tabla de complejidades comunes
| Complejidad | Nombre | Ejemplo |
|---|---|---|
| O(1) | Constante | arr[0] |
| O(log n) | Logarítmica | Búsqueda binaria |
| O(n) | Lineal | Recorrer un arreglo |
| O(n log n) | Lineal logarítmica | Merge Sort |
| O(n^2) | Cuadrática | Bucles anidados |
| O(2^n) | Exponencial | Recursión sin control |
| O(n!) | Factorial | Permutaciones completas |
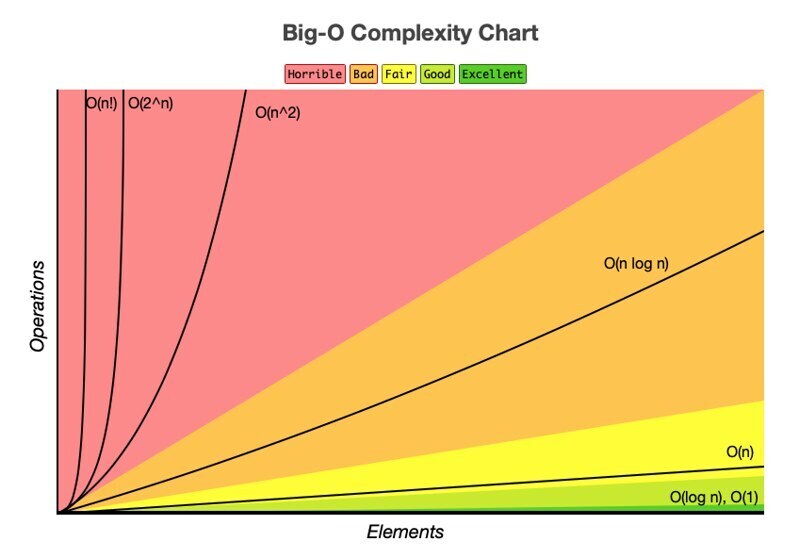
[Referencia]: https://www.scribd.com/document/510753315/Big-O-Algorithm-Complexity-Cheat-Sheet-Know-Thy-Complexities
4. Ejemplos paso a paso en Java
// O(1)
int obtenerPrimero(int[] arr) {
return arr[0]; // Siempre es una sola operación
}
// O(n): recorrer arreglo
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
// O(log n): búsqueda binaria
int izq = 0, der = arr.length - 1;
while (izq <= der) {
int mid = (izq + der) / 2;
if (arr[mid] == x) return true;
else if (arr[mid] < x) izq = mid + 1;
else der = mid - 1;
}
// O(n log n): Usando Arrays.sort
void ordenar(int[] arr) {
Arrays.sort(arr);
}
// O(n²) — Cuadrática
void compararTodos(int[] arr) {
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr.length; j++) {
System.out.println(arr[i] + " vs " + arr[j]);
}
}
}
// O(n!) — Factorial
void permutar(String str, String resultado) {
if (str.length() == 0) {
System.out.println(resultado);
return;
}
for (int i = 0; i < str.length(); i++) {
permutar(str.substring(0, i) + str.substring(i + 1), resultado + str.charAt(i));
}
}5. Regla para combinar complejidades
- Si están uno tras otro → se suman: O(n + n) = O(2n) → O(n)
- Si están anidados → se multiplican: O(n * n) = O(n^2)
▶ Caso 1: operaciones una tras otra
for (...) { ... } // O(n)
for (...) { ... } // O(n)→ O(n + n) = O(2n) = O(n) (constantes se ignoran)
▶ Caso 2: operaciones anidadas
for (...) {
for (...) {
...
}
}→ O(n * n) = O(n^2)
Esto funciona para cualquier tipo de complejidad: lineal, logarítmica, exponencial, etc.
6. Veamos ejemplos:
Regla 1: Si las operaciones están una tras otra → se SUMAN
public void procesar(int[] arr) {
// Primera parte
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
// Segunda parte
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i] * 2);
}
}▶ Análisis:
- Primer for: O(n)
- Segundo for: O(n)
- Total: O(n) + O(n) = O(2n) ▶ Pero en Big-O se eliminan constantes → O(2n) = O(n)
▶ Otro ejemplo:
public void procesoMixto(int[] arr) {
System.out.println("Inicio"); // O(1)
for (int i = 0; i < arr.length; i++) { // O(n)
System.out.println(arr[i]);
}
System.out.println("Fin"); // O(1)
}- Total: O(1) + O(n) + O(1) = O(n + 2) → O(n)
Regla 2: Si las operaciones están anidadas → se MULTIPLICAN
public void compararTodos(int[] arr) {
for (int i = 0; i < arr.length; i++) { // O(n)
for (int j = 0; j < arr.length; j++) { // O(n)
System.out.println(arr[i] + "," + arr[j]);
}
}
}▶ Análisis:
- El for interno se ejecuta n veces por cada iteración del externo.
- Total: O(n) * O(n) = O(n²)
▶ Otro ejemplo anidado:
public void tripleBucles(int[] arr) {
for (int i = 0; i < arr.length; i++) { // O(n)
for (int j = 0; j < arr.length; j++) { // O(n)
for (int k = 0; k < arr.length; k++) {// O(n)
System.out.println(i + j + k);
}
}
}
}- Total: O(n * n * n) = O(n³)
▶ Otro ejemplo:
void algoritmoRamdon(int[] arr) {
int n = arr.length;
for (int i = 0; i < n; i++) {
int j = i;
while (j > 0) {
j = j / 2;
System.out.println(j);
}
}
}▶ Paso a paso:
- El bucle externo (for) corre n veces: desde i = 0 hasta i = n-1 → O(n)
- Dentro de ese bucle, hay otro bucle (while) que divide j entre 2 en cada paso, es decir: Para un valor i, el while hace: i → i/2 → i/4 → ... → 1 → 0 Esto se ejecuta log₂(i) veces (porque estás dividiendo entre 2 hasta llegar a 0).
▶ ¿Entonces cuánto tarda en total?
Cada iteración del for hace log i pasos → debemos sumar eso para todos los i:
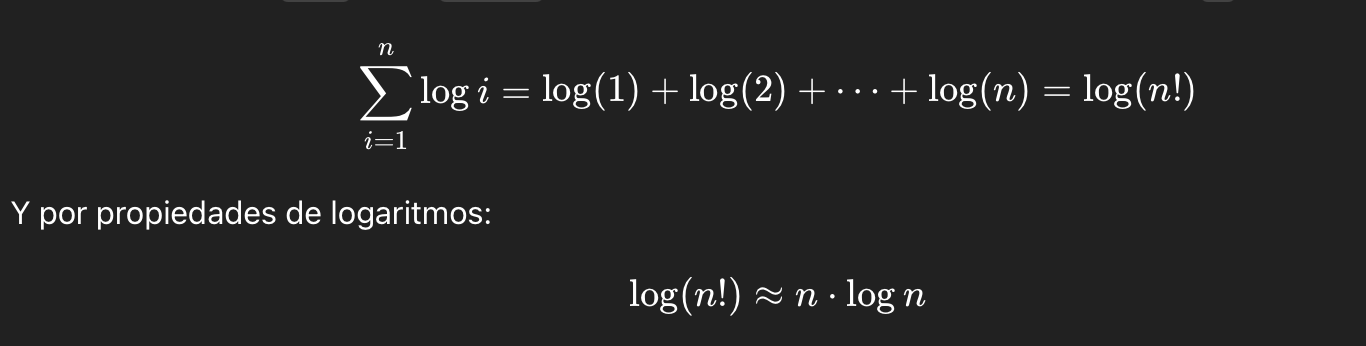
▶ Resultado final: O(n log n)
7. Complejidad espacial (uso de memoria)
No se mide en KB exactos, sino en proporción al tamaño de la entrada:
| Notación | Significado | Ejemplo |
|---|---|---|
| O(1) | Memoria constante | Solo variables simples |
| O(n) | Memoria lineal | Copiar arreglo |
| O(n^2) | Memoria cuadrática | Matriz n x n
|
8. Preguntas frecuentes que también tuve:
- ¿Por qué se ignoran las constantes? Porque no afectan el crecimiento para
ngrande. - ¿Y si hago tres bucles separados? Se suman.
- ¿Y si hago uno dentro de otro? Se multiplican.
- ¿Puedo sumar O(log n) + O(n)? Sí, pero el mayor gana: O(n + log n) = O(n)