Antes de la llegada de Zero Knowledge, ya existían algunas aplicaciones que lograban mantener cierta privacidad on-chain. Algunos ejemplos son el juego Cheese Wizards, el sistema de votaciones de Kleros o DutchX el sistema de subastas creado por Gnosis, entre otros proyectos que exploraron formas creativas de mantener datos ocultos a la vista pública de on-chain. En este artículo, vamos a estudiar de forma teórica y práctica el esquema Commit-Reveal, una técnica sencilla pero con bastante alcance que hace esto posible. Exploraremos su funcionamiento, sus limitaciones y algunos errores comunes al implementarlo.
“Adivina el número”: un juego 100% en Solidity
Para ilustrar este esquema de forma clara, vamos a construir un pequeño juego: “Adivina qué número estoy pensando”. Será una aplicación completamente on-chain, escrita únicamente en Solidity y que guarda datos privados sin necesidad de usar ZK.

En este tutorial vamos a construir un contrato de "Adivina el número".
Este juego nos permitirá introducir conceptos fundamentales como las funciones hash, que son la base de los commitments (respaldos o compromisos) usadas por este esquema.
Funciones hash
Una función hash es una función determinista que toma una entrada y produce una salida que aparenta ser aleatoria pero no lo es. Lo importante aquí es que estas funciones son irreversibles: es fácil calcular hash(a) → b, pero prácticamente imposible deducir a a partir de b.
Este comportamiento las hace ideales para almacenar secretos. Ethereum utiliza funciones hash como keccak256 en muchos contextos: desde la generación de claves públicas, hasta la construcción de bloques o el uso de mappings dentro de contratos.
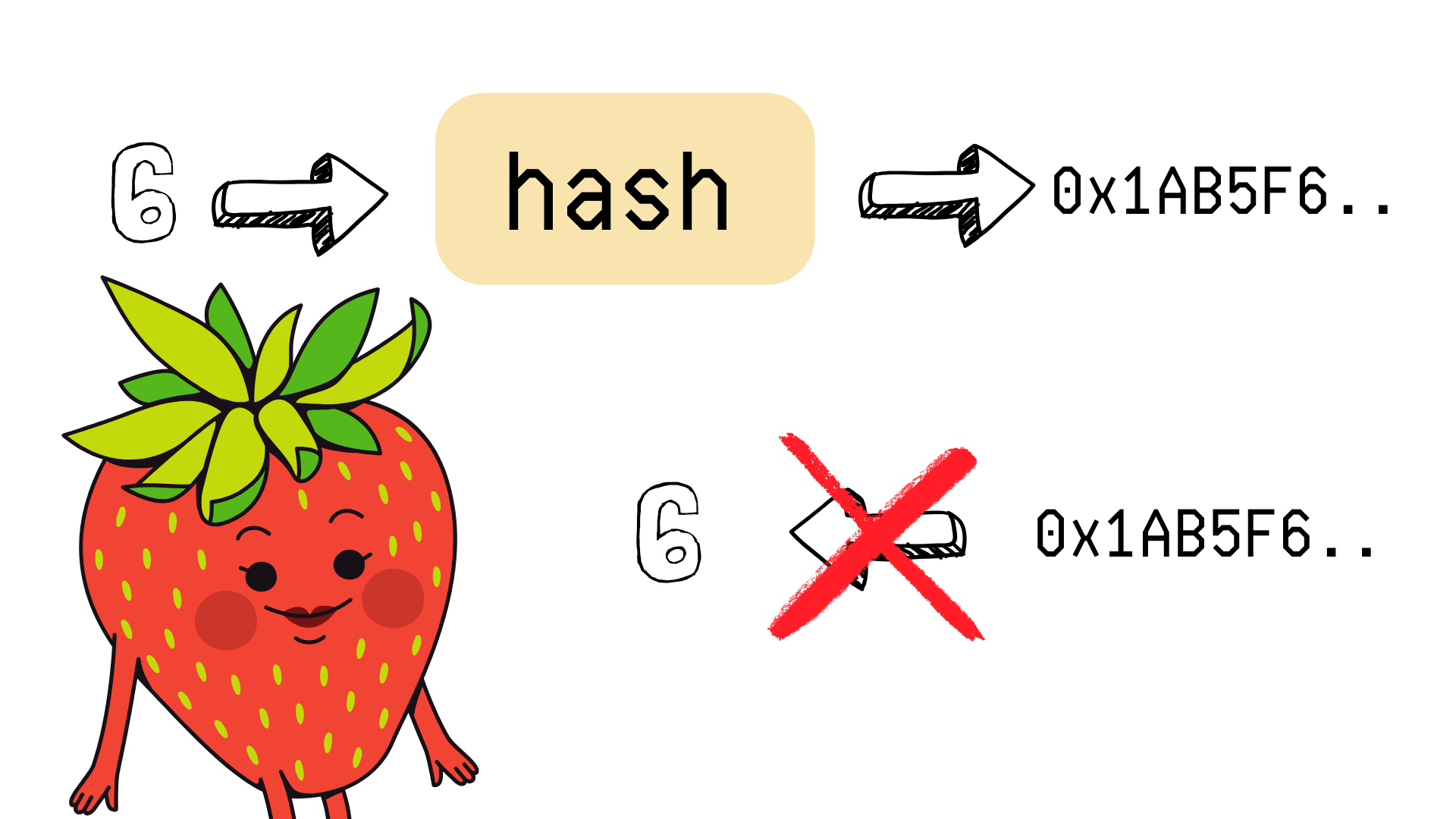
A partir del hash de un valor no podemos deducir el valor original.
Adivina el número: versión ingenua
Veamos ahora una primera versión del juego en Solidity, que si bien funciona, tiene muchos problemas. ¿Puedes ver cuáles son?
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.22;
// Contrato de un ahorcado ingenuo: sujeto a diversos ataques
contract SimpleNumberGuess {
// Has del número secreto
bytes32 public numberCommitment;
// Address del ganador del juego, quien lo adivine primero
address public winner;
// El juego inicia almacenando el hash del número por adivinar
constructor(bytes32 _numberCommitment) {
numberCommitment = _numberCommitment;
}
// Cualquier jugador participa eligiendo un número, el primero en adivinar será registrado como el ganador
function guessNumber(uint8 guess) public {
require(hashFunction(guess) == numberCommitment, "Invalid number");
require(winner == address(0), "Number already guessed");
winner = msg.sender;
}
// Función hash que usaremos para hashear y ocultar el número
function hashFunction(uint8 value) public pure returns (bytes32) {
return keccak256(abi.encodePacked(value));
}
}El contrato parece hacer lo correcto, guarda el hash del número secreto y permite que los jugadores lo adivinen. Pero en realidad presenta varias fallas graves.
Por un lado, cualquiera podría simplemente probar todos los números posibles (del 0 al 255 si usamos uint8) hasta encontrar uno cuyo hash coincida. Este ataque por fuerza bruta se vuelve facil de realizar si no protegemos el número con un salt.
Por otro lado, como las adivinanzas se envían en transacciones públicas, cualquier jugador podría ser frontrunneado (adelantado en la mempool por alguien que paga más gas) si su elección es la correcta.
Miremos entonces cómo el esquema Commit-Reveal lo soluciona.
¿Qué es el esquema Commit-Reveal?
El Commit-Reveal es una técnica muy común en criptografía que permite a una parte comprometerse con un valor sin revelarlo hasta un momento posterior. Se divide en dos fases:
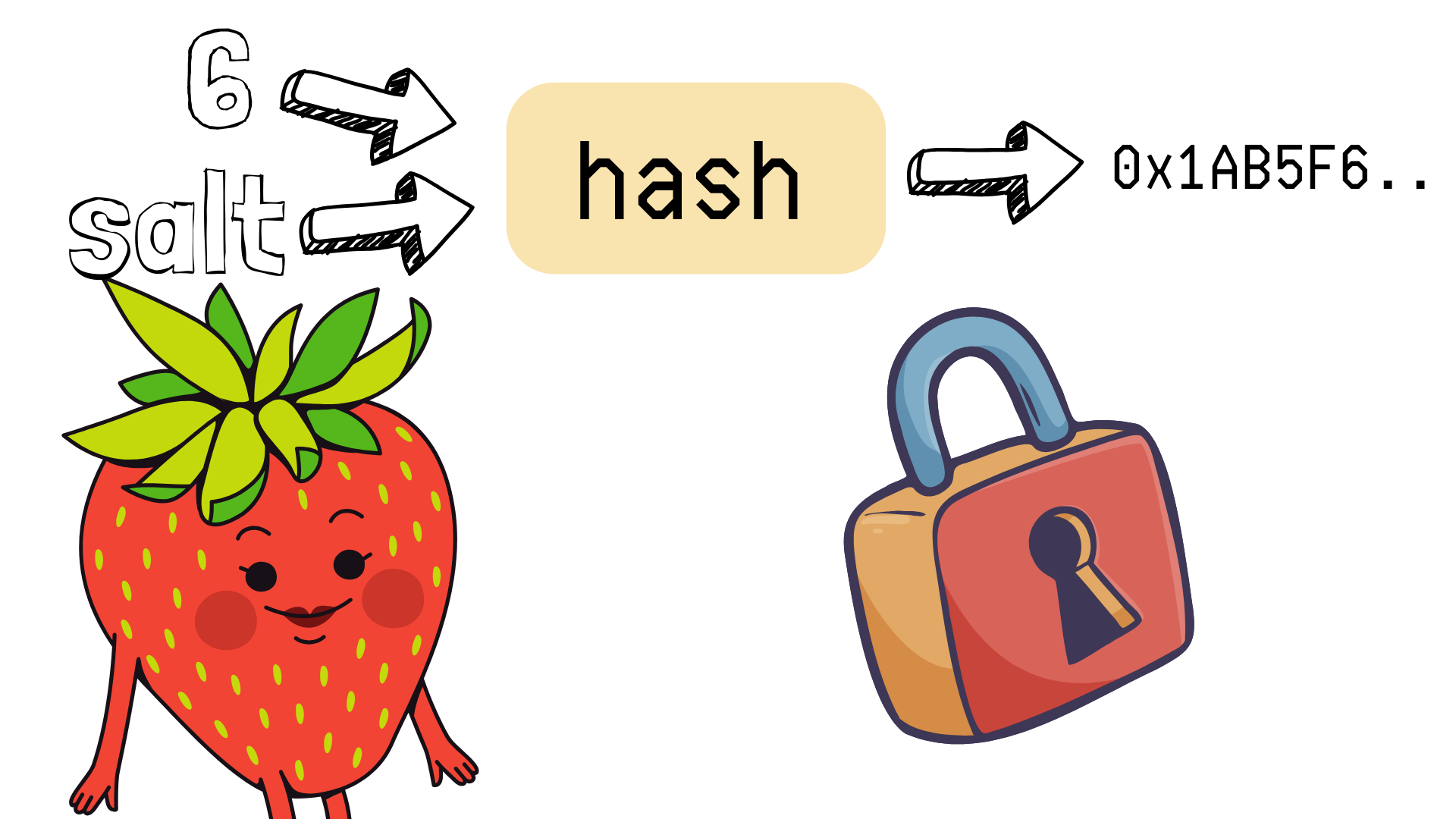
- Commit: Se publica el hash de un dato junto con un salt secreto. Este hash es el commitment.
- Reveal: Más adelante, se revelan el dato y el salt. Cualquiera puede verificar que coinciden con el hash publicado anteriormente.
Veamos cómo se aplicaría esto en nuestro juego de “Adivina el número”.
Etapa 1: El Commit
El administrador del juego selecciona un número secreto y un salt aleatorio. Luego, calcula el hash de ambos usando keccak256 (función hash que viene en Ethereum por defecto) y lo publica en el contrato. Este valor será inmutable durante el resto del juego.
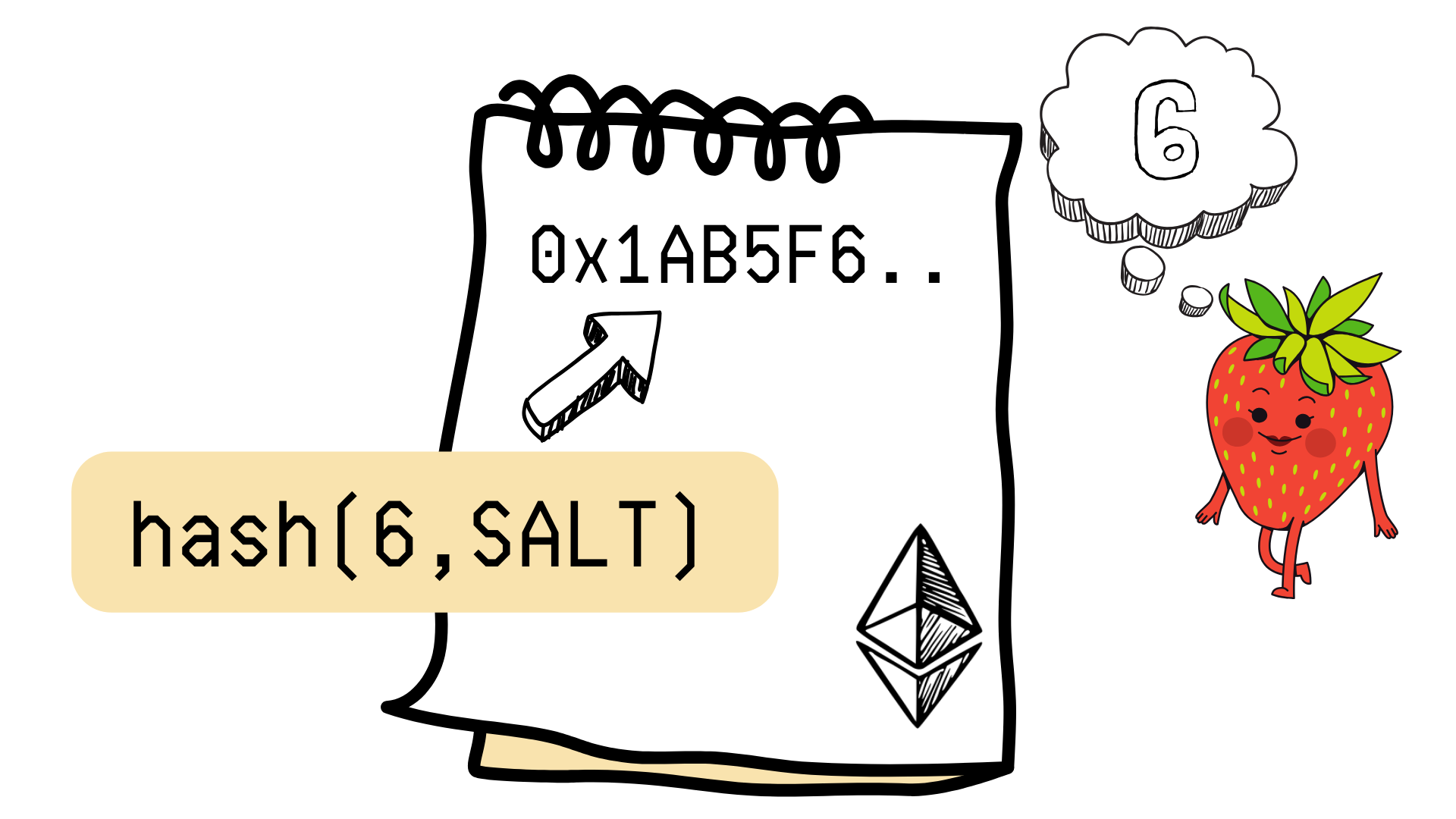
Etapa 2: Registro de participantes
Los jugadores eligen públicamente un número del 0 al 10. Este paso no requiere privacidad, por lo que pueden hacerlo directamente on-chain.
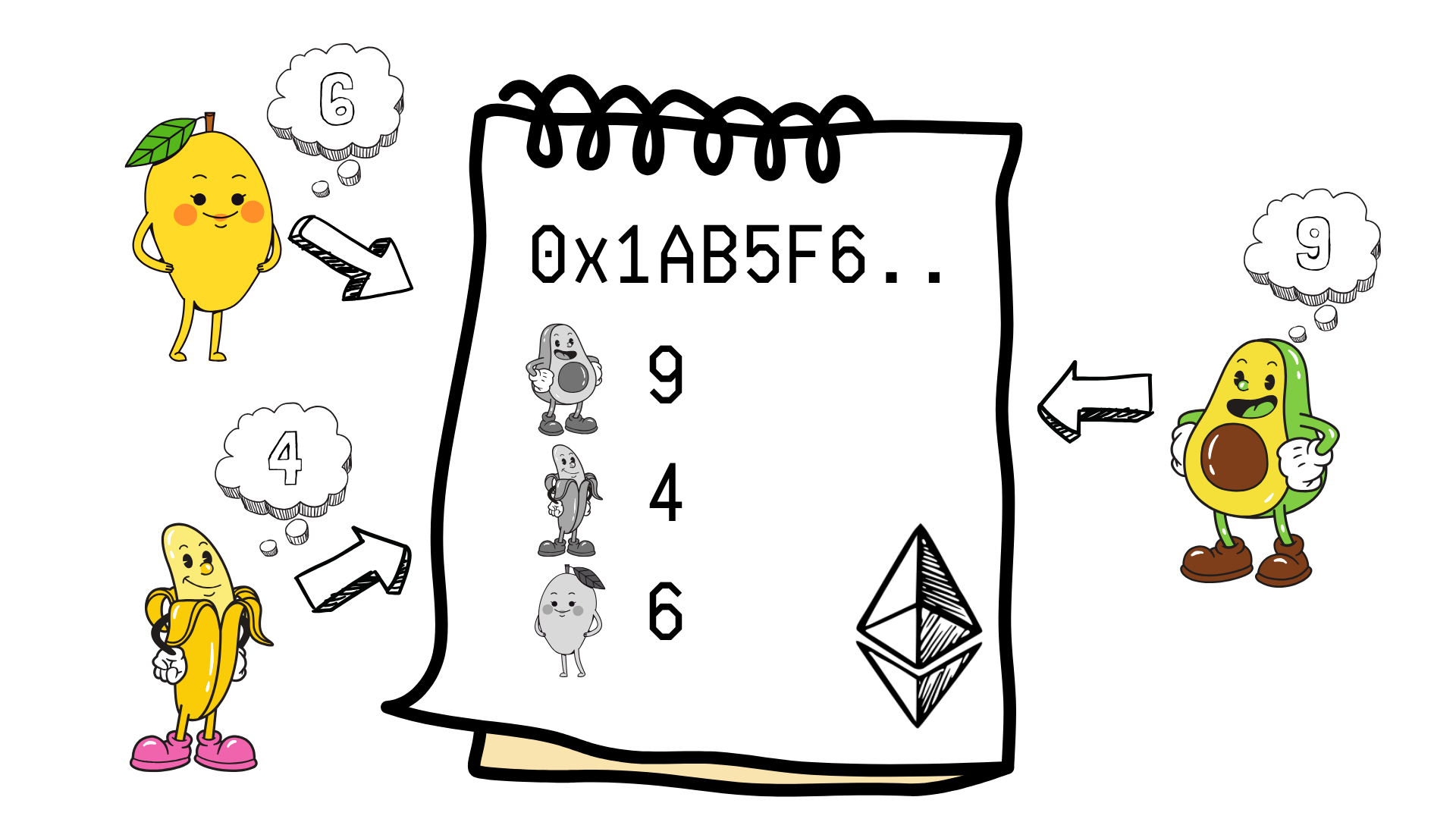
Etapa 3: El Reveal
Cuando termina el tiempo de juego, el administrador revela el número original y el salt. El contrato vuelve a calcular el hash y verifica que coincide con el commitment inicial.
Si todo es válido, se puede declarar al ganador.
Implementación completa del juego con Commit-Reveal
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.22;
// Contrato ejemplo de esquema commit-reveal
// Consiste en el juego de "Adivina cuál número del 0 al 10 estoy pensando"
contract SimpleNumberGuess {
// Hash commitment of the secret number (capped via modulo 11)
bytes32 public numberCommitment;
// Flag que indica si el número ya fué revelado
bool public revealed;
// Número revelado, debe ser un número entro 0 a 10
uint8 public secretNumber;
// Almacena los addresses de los jugadores, únicamente un address por número
mapping(uint8 => address) public guessers;
// Al iniciar el juego enviamos el commitment del juego tal que numberCommitment = keccak256(número oculto, SALT)
constructor(bytes32 _numberCommitment) {
numberCommitment = _numberCommitment;
}
// Cualquier jugador puede participar siempre y cuando el juego ya inició, el número sea entre 0 y 10 y nadie más lo haya seleccionado
function guessNumber(uint8 _guess) public {
require(!revealed, "Game already revealed");
require(_guess <= 10, "Guess must be between 0 and 10");
require(guessers[_guess] == address(0), "Number already taken");
guessers[_guess] = msg.sender;
}
// El número secreto es revelado hasheando de nuevo el número oculto junto con el salt y verificando que sea igual al commitment guardado anteriormente
// Únicamente el creador del juego debería ser capáz de revelar el número secreto pues para hacerlo deberá revelar también el salt
function reveal(uint8 number, uint256 salt) public {
// El commitment debe ser igual al hash del número junto con el salt
require(hashFunction(number, salt) == numberCommitment, "Invalid reveal");
// Nos aseguramos que el número secreto sea un número entre 0 y 10 al hacer modulo 11
// Este es un ejemplo sencillo y en realidad podemos omitir el salt pues usamos modulo, pero en casos mas avanzados sí es necesario para evitar ataques de fuera bruta
secretNumber = number % 11;
revealed = true;
}
/// Una vez terminado el juego podemos verificar quién es el ganador
function checkWinner() public view returns (address) {
require(revealed, "Number not revealed yet");
return guessers[secretNumber];
}
/// Funcion hash que usamos off-chain para crear un commitment, y también on-chain para verificarlo
function hashFunction(uint8 value, uint256 salt) public pure returns (bytes32) {
return keccak256(abi.encodePacked(value, salt));
}
}Limitaciones del esquema Commit-Reveal
Aunque funciona y provee mucha utilidad, este esquema tiene limitaciones importantes. Una de ellas es que no existe garantía de que el dato será revelado. Si quien realizó el commitment no publica el dato y el salt, el juego simplemente queda inconcluso. Este es un problema de liveness.
Una solución que no es perfecta pero puede funcionar consiste en requerir que quien hace el commit deposite una cantidad de ETH que sólo podrá recuperar si realiza el reveal dentro de cierto plazo.
Otra limitación importante es que no se puede validar la veracidad o validez de los datos privados hasta que se revelan. No hay forma de aplicar lógica sobre esos datos durante la etapa de commit.
Ahí es donde las pruebas ZK ofrecen una mejora significativa pues permiten demostrar que un dato privado cumple ciertas condiciones, sin necesidad de revelarlo. Pero eso lo veremos en la siguiente artículo.
¡Gracias por ver este artículo!
Sígueme en dev.to y en Youtube para todo lo relacionado al desarrollo en Blockchain en Español.
