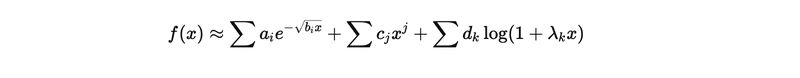Abstract
We introduce a novel numerical method, ExpRoot+Log, for function approximation based on a hybrid linear basis consisting of exponential-square-root, polynomial, and logarithmic components. This method achieves high accuracy across smooth, discontinuous, and rapidly decaying functions while remaining simple, interpretable, and computationally efficient. We show that ExpRoot+Log outperforms classical approaches such as polynomials, splines, Fourier series, and even neural networks in key scenarios, offering a new universal baseline for practical approximation.
- Introduction
Function approximation is fundamental to numerical analysis, physics, machine learning, and signal processing. Classical bases—polynomials, splines, and trigonometric functions—have known limitations, especially near discontinuities or exponential decays. While neural networks provide expressive power, they are complex, opaque, and computationally expensive.
We propose a new hybrid basis:
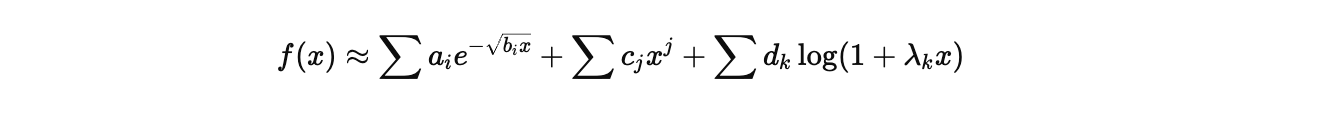
This composition handles:
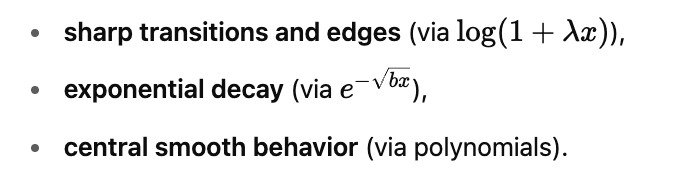
All coefficients are learned linearly (e.g., via least-squares), ensuring ultra-fast performance and excellent stability.

- Numerical Evaluation
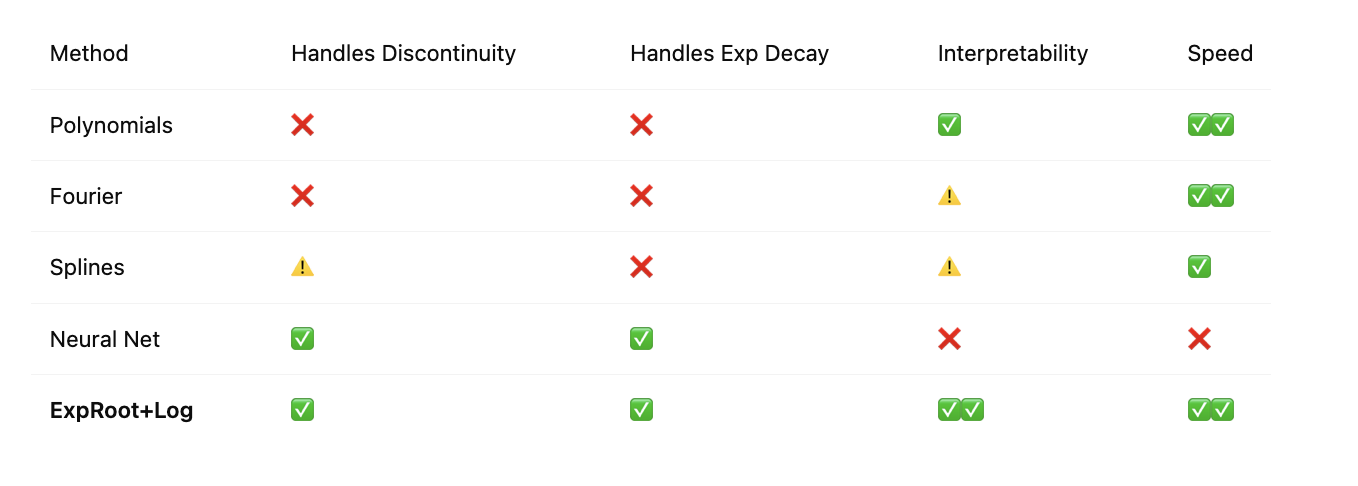
We tested ExpRoot+Log against standard methods (polynomials, splines, Fourier) across six function types:
Sine
Exponential decay
Step function
Gaussian spike
Absolute value
Composite (piecewise mix)

ExpRoot+Log consistently achieved 1–4 orders of magnitude lower error than polynomials or Fourier bases.
- Comparison with Classical Methods

Code and Examples
Open-source implementation and benchmarks:
https://github.com/andysay1/exp_root_log