Remember those sine, cosine, and tangent functions from math class? The ones associated with right triangles and scary formulas? If they made your head spin (pun intended), you’re not alone. But despite their intimidating reputation, these functions are surprisingly everywhere — in the music you listen to, the way things move in games and animations, even in how your browser can style a bouncing ball. In this Medium-style tour, we’ll demystify sine, cosine, and tangent (and even their inverses) in plain English. No deep math background needed — just your curiosity. By the end, you’ll see how these “trig” functions form the language of circles and waves that powers much of our digital world.
Sine, cosine, and tangent — In plain english
Let’s start with the basics: sine , cosine , and tangent are three functions that relate angles to ratios. That sounds abstract, so imagine a simple scenario: take a right triangle (one angle 90°). Pick one of the other angles and call it θ (theta). Now, sine and cosine are basically telling you how “tilted” that angle is in terms of vertical and horizontal components. In fact, sin(θ) is defined as the ratio of the triangle’s height to its slanted side (opposite/hypotenuse), and cos(θ) is the ratio of the base to the slanted side (adjacent/hypotenuse). If those definitions don’t stick, it’s okay – just picture a circle:
- Sine of an angle gives the vertical component (how far up or down you are on a circle).
- Cosine of an angle gives the horizontal component (how far right or left you are on a circle).
- Tangent of an angle is a bit different — it’s essentially sine divided by cosine (vertical divided by horizontal). It tells you the slope or steepness corresponding to that angle.
What’s cool is that no matter the size of the triangle or circle, these ratios come out the same for the same angle. Spin around a circle and watch the sine and cosine values: they will always oscillate between -1 and 1. At 0° (facing right on the circle), cos is 1 and sin is 0. At 90° (facing up), sin is 1 and cos is 0. At 180° (left), cos = -1, sin = 0. At 270° (down), sin = -1, cos = 0. By 360° you’re back where you started, and the cycle repeats.
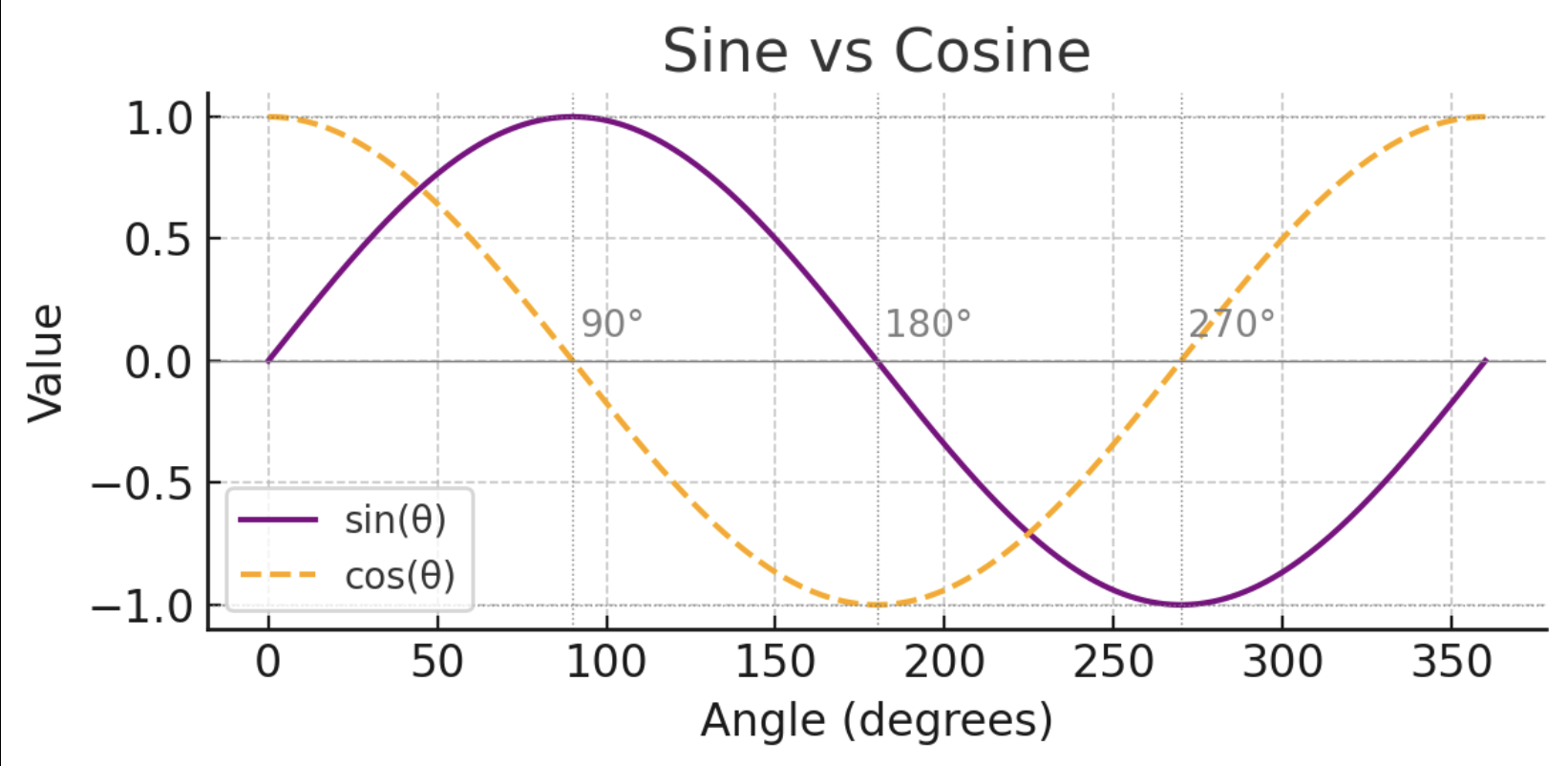
Figure: A comparison of the sine function (purple curve) and cosine function (orange dashed curve) over one full cycle (0° to 360°). Notice how cosine is just a shifted version of sine — at 0° cosine is 1 while sine is 0, and by 90° they’ve swapped. Both functions smoothly oscillate between -1 (minimum) and 1 (maximum). Sine starts at 0 and rises to 1 by 90°, whereas cosine starts at 1 and dips to 0 by 90°.
You can see from the figure that sine and cosine are like twin waves — cosine is essentially the same wave as sine, just shifted 90° in phase. Both are nice smooth curves. In contrast, tangent is a bit of a wild one: since it’s sin(θ)/cos(θ), whenever cos(θ) gets close to 0 (like near 90° or 270°), the tangent shoots off to very large values (or negative large) – in math speak, it has asymptotes (it blows up to infinity). Tangent is 0 at 0° (because sin(0)/cos(0) = 0/1 = 0), and by 45° tan = 1 (sin and cos are equal there). If you graph tangent it looks different – it doesn’t oscillate up and down like sine/cos; instead it goes up, down, up, down, repeating every 180° with those infinite spikes in between. But don’t worry: in everyday applications we rarely need the crazy parts of tangent, mostly we use it (or its inverse) to get angles or slopes , as we’ll see.
Key takeaway: Sine and cosine handle the smooth wave-like motion (bounded between -1 and 1), and tangent relates to slope (and can grow unbounded). Next, we’ll explore why these are super useful outside of geometry class.
What about the inverses (arcsin, arccos, arctan)?
Sometimes you have the result of a trig function and want to find the angle that produced it. That’s where inverse trig functions come in. The inverse of sine is arcsine (often written asin or sin⁻¹), the inverse of cosine is arccosine (acos), and the inverse of tangent is arctangent (atan). Inverse here means they “undo” the original function. For example, if sin(30°) = 0.5, then arcsin(0.5) = 30° (in general, arcsin 0.5 could also give 150°, but by convention arcsin returns the angle in the range –90° to +90°). These inverse functions output an angle.
Arctan (also called atan2 when taking two coordinates) is particularly handy in computing and graphics: if you know the horizontal and vertical components of a direction (say a joystick’s x and y or a point’s coordinates), arctan tells you the angle of that direction. In other words, if tan(θ) = opposite/adjacent, then θ = arctan(opposite/adjacent). This is how, for instance, your phone might compute the tilt angle from accelerometer readings, or how a game figures out that your character should turn 75° to face the target at (x,y). We won’t focus too much on the inverses, but it’s good to know they’re there whenever you need to go from a ratio back to an angle.
Waves everywhere: Sine in sound and nature
One of the most fascinating things about the sine function is that it appears everywhere in nature and technology as a fundamental wave shape. A sine wave is the purest form of a repeating oscillation. If you pluck a guitar string or play a single note on a keyboard, the sound you hear can be approximated by a sine wave of a certain frequency. The air molecules vibrate back and forth smoothly — if you graphed the air pressure changes over time, it’d trace out that familiar wavy sine curve. In fact, sine waves occur often in physics — from ocean waves to sound waves and even light waves. A pure tone (like a tuning fork’s note) is essentially a sine wave of air pressure.

Your speakers work by moving in and out in a sinusoidal pattern for each pure tone frequency. Why sine? Because it’s a naturally smooth oscillation. Sine is the epitome of a smooth, natural sway. Springs bouncing, pendulums swinging, and atoms vibrating — they all follow (approximately) sinusoidal motion. If you’ve ever seen a graph of a calm heartbeat or a smooth periodic signal, chances are it’s a sine-like shape. Nature loves sine waves because they’re stable and clean; any complicated vibration can actually be broken down into a bunch of sine waves added together (this is called Fourier analysis, which is beyond our scope, but it’s amazing!). So next time you hear a pure musical note or see gentle waves on a pond, you’re experiencing sine (and cosine) in action.
Smooth animations: Using sine in web design
So far, we’ve talked about how trig functions describe movements and waves in the real world. Now let’s look at how they’re used in the digital world — specifically in web development and animations. If you’re a web developer or just a visually inclined tech user, you’ve likely seen or created animations that move things around on the screen. Ever notice how good animations don’t move at a constant, robotic speed? Instead, objects often ease in and out of motion — starting slowly, speeding up, then slowing down smoothly to a stop. Guess what underlies many of those smooth motions? Yep, sine (and cosine) curves! A sine wave’s shape — slow at the top, fast through the middle, slow at the bottom — is perfect for creating natural-feeling movement. In fact, an “ease-in-out” timing in CSS or JavaScript animations often mimics a half-sine wave for the speed curve. The object moves fastest at mid-cycle and pauses momentarily at the turn-around points, much like a pendulum. This is far more realistic than a linear start-stop. Many animation libraries use sinusoidal easing functions under the hood to achieve this fluid effect. One author describes it well: linear motion feels constant and abrupt, whereas sine motion eases naturally, like a dance — speeding up, then slowing down gracefully, consider making a ball bob up and down on a webpage. We can use CSS animations to achieve this with a sine-like smoothness. Here’s a quick snippet:
.ball {
width: 50px;
height: 50px;
background: tomato;
border-radius: 50%;
/* Animate the ball with a bobbing motion */
animation: bob 2s infinite ease-in-out;
}
@keyframes bob {
0% { transform: translateY(0); } /* start at original position */
50% { transform: translateY(-50px); } /* move up by 50px at halfway */
100% { transform: translateY(0); } /* back to start */
}This CSS animation named bob moves an element (like a div with class "ball") up and then back down. The ease-in-out timing makes the movement slow down at the top and bottom, approximating that smooth sine-wave vibe. The result is a gentle up-and-down bobbing, as if the ball is attached to an invisible spring. If it were linear (animation-timing-function: linear), the ball would abruptly switch direction at the top, looking mechanical. With the easing (which is essentially using part of a sine curve), it pauses for a split second at the peak before descending.
Modern web tech even takes this a step further: CSS has gained built-in trigonometric functions! You can now directly use sin(), cos(), tan() and their inverses in CSS calculations. This means you could, for instance, position elements in a circle or create oscillating motions without any JavaScript, purely with CSS math. For example, you might see something like:
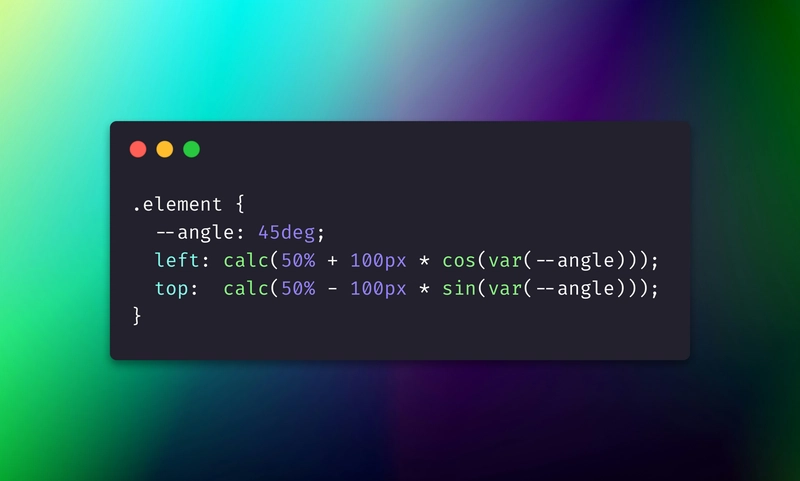
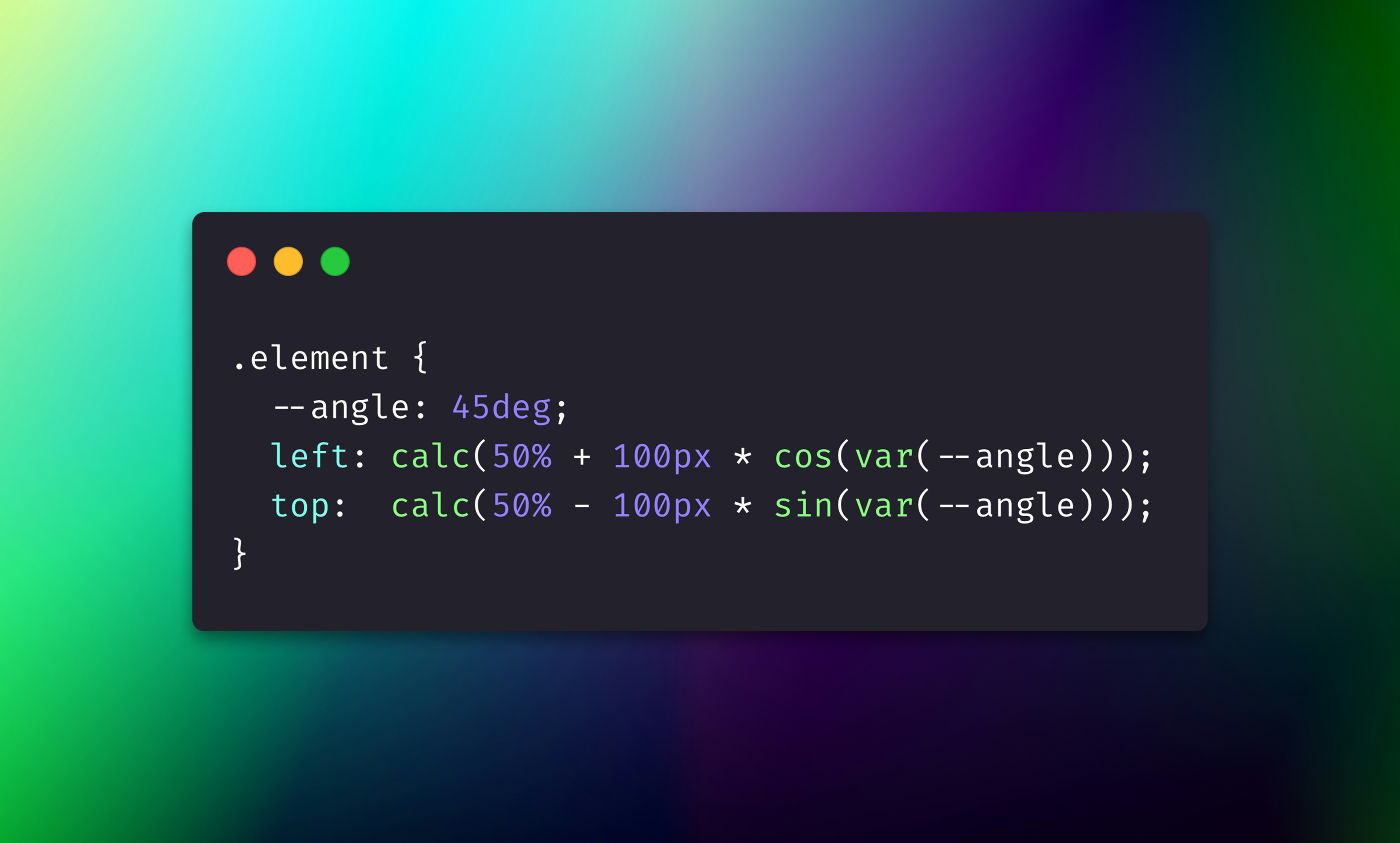
.element {
--angle: 45deg;
left: calc(50% + 100px * cos(var(--angle)));
top: calc(50% - 100px * sin(var(--angle)));
}In this snippet, --angle is a CSS variable (here 45°). The element’s left and top positions are calculated using cosine and sine of that angle, effectively placing the element on a circle of radius 100px around the center (50%,50% of the parent). If you then animate --angle from 0° to 360° (CSS can do this via custom property animation), the element would move in a perfect circle. How cool is that? 🎉 In the past, you’d have needed JavaScript to update the position each frame; now the browser can do it natively with CSS. This kind of capability is cutting-edge (part of the CSS Values and Units Level 4 spec), but it’s already available in modern browsers and showcases how important trig functions are even in styling web pages.
You can find another example on my project csstoday.dev
Even without writing CSS from scratch, if you use any no-code or low-code animation tools, when you choose a “circular motion” or a “pendulum swing” preset, you’re indirectly using sine and cosine. If you use a library like GSAP or anime.js and pick a sine easing, you’re literally saying “use a sine function to interpolate this motion.”
Conclusion
Trigonometric functions might have started as the study of triangles and circles, but they’ve grown into fundamental tools for describing the world — both physical and digital. Sine, cosine, and tangent are the math behind the music we hear, the waves we see, and the smooth animations we enjoy on our screens. They allow us to move from angles to coordinates and back again, making them indispensable for game developers, animators, engineers, and even hobbyist tinkerers.
Hopefully, this friendly overview shed some light on these functions without giving you a math headache. The next time you see a bouncing icon, a rotating graphic, or hear a clear musical tone, you’ll know that trig functions are quietly at work behind the scenes. Trigonometry is truly the hidden pattern in so many things around us. So here’s to sine, cosine, and tangent — the unsung heroes that make our digital (and natural) worlds go round (and round)! Happy observing, and happy coding if you’re inspired to put these functions to use in your own creative projects.