So I tried Quantum Computing. For the past few years, I had been hearing a lot about quantum computing and how modern it is, with claims that it's going to change the world by solving very complex problems in just seconds.
However, I was always afraid to dive deep and understand what it actually is. In my first year, I was introduced to quantum computing during a session. That session made me realize how far we have come in the research domain and how companies like IBM, Google, and others are working on it.
I was excited, but I was scared to even look into the technical details because I had tried learning quantum physics in my 12th grade and thought it would be similar and boring. That was until a notification popped up that our college's computer science department was organizing a workshop. I instantly registered for it because I believe it is always easier to work on things when someone or something pushes us.
Here are my learnings and the things I got to know, along with my own observations, This will help you get a basic idea about what this is all about at the technical level just to make you curious and get interested in this
Qubit
In classical computing, all information and data are ultimately reduced to binary form, stored as a series of 0s and 1s. Each unit that can represent either 0 or 1 is called a bit.
In quantum computing, however, the concept of binary doesn't apply in the same way. Here, the value can be 0, 1, or even both 0 and 1 at the same time (Isn't this fascinating!!). This value is called a qubit.
You can think of a qubit as the quantum equivalent of a bit. Qubits are created by manipulating and measuring quantum particles such as photons, electrons, trapped ions, and atoms, which we need not worry about right now.
Quantum Properties
To fully appreciate the power of qubits, we must know the quantum properties that govern their operations:
Superposition
Qubits show the property of superposition. Superposition is a core principle that allows quantum bits, or qubits, to exist in multiple states at once. A quantum state can be shown by this equation where it is represented as a matrix, and also in Dirac notation, where α and β are complex numbers representing the probability amplitudes for the qubit to be in ∣0⟩ and ∣1⟩, respectively.

So, for example, this state represents a qubit in an equal superposition of ∣0⟩ and ∣1⟩, with a 50% chance of measuring either state.
Superposition in Ant-Man
I researched and looked into the Ant-Man character in Marvel, which loosely takes inspiration from quantum mechanics. For example, in Ant-Man and the Wasp: Quantumania, when Ant-Man shrinks down to the subatomic level and enters the Quantum Realm, the visual depiction often shows multiple, overlapping realities or versions of him. This can be interpreted as a loose representation of quantum superposition, where Scott Lang’s existence becomes uncertain, spread across multiple possible states.
Entanglement
When two particles remain connected even when separated by vast distances, this phenomenon is called quantum entanglement. When two qubits (quantum bits) are entangled, their states are not independent. Instead, they share a single, unified quantum state. For example, if you have two entangled qubits, the state of one qubit can't be described without considering the state of the other. Entanglement allows quantum computers to manipulate many qubits in a single operation, instead of manipulating each qubit individually, as in classical computing.
Entanglement in Ant-Man

Again, if you relate it to Ant-Man, in the first Ant-Man movie, Scott Lang briefly enters the Quantum Realm and forms a connection with Janet Van Dyne, who has been trapped there for decades. This link, called "quantum entanglement," suggests their minds are connected across space and time. It's a fictionalized version of quantum entanglement, where two particles or objects are linked in a way that the state of one directly affects the other, no matter the distance.
Interference
In quantum computing, interference refers to how quantum states can combine or cancel each other out, similar to how waves interact. This is used to manipulate the probabilities of different outcomes, helping quantum computers solve problems more efficiently by amplifying the correct answers and reducing the chances of wrong ones.
Quantum Gates
Quantum Gates are the most important building blocks in quantum computing. Quantum gates are similar to classical gates, but the difference is that they operate on qubits, along with a few other differences.
If you want to understand this in detail, refer to the Bloch sphere, which will help you visualize quantum states.
I’m taking few gates here for simplicity:
X Gate (Pauli-X):
The X gate is equivalent to the classical NOT gate. When applied to a qubit, it flips its state: ∣0⟩ becomes ∣1⟩, and ∣1⟩ becomes ∣0⟩. This is a direct analogy to the classical logic gate, where a NOT gate inverts the bit (0 to 1 and vice versa).
Y and Z gates:
it manipulate the y and z axes of the Bloch sphere, which represent different aspects of the qubit’s state. While the X gate affects the qubit on the x-axis, the Y gate rotates the qubit around the y-axis, and the Z gate rotates it around the z-axis.
Hadamard Gate (H Gate):
This is one of the most important gates in quantum computing because it creates a superposition state. When applied to a qubit in the ∣0⟩ state, the Hadamard gate transforms it into a superposition of both ∣0⟩ and ∣1⟩. After the Hadamard gate is applied, the qubit has a 50% chance of being measured as ∣0⟩ and a 50% chance of being measured as ∣1⟩. The Hadamard gate is essential for many quantum algorithms because it generates the probabilistic nature that allows quantum computers to explore multiple outcomes simultaneously.
Controlled NOT (CNOT) Gate
The CNOT gate is a multi-qubit gate, meaning it applies to two or more qubits at once. It is particularly important in creating quantum entanglement. The CNOT gate operates on two qubits: a control qubit and a target qubit. If the control qubit is in the state ∣1⟩, the gate flips the state of the target qubit (i.e., it applies an X gate to the target qubit). If the control qubit is ∣0⟩, the target qubit remains unchanged. This conditional operation is what makes the CNOT gate crucial for quantum logic and entanglement between qubits.
Simulating a Quantum Circuit
This is where we apply quantum gates to qubits and perform operations. Below is a quantum circuit made using an X gate, a Hadamard gate, and a CNOT gate. This circuit is also known as a Bell state:
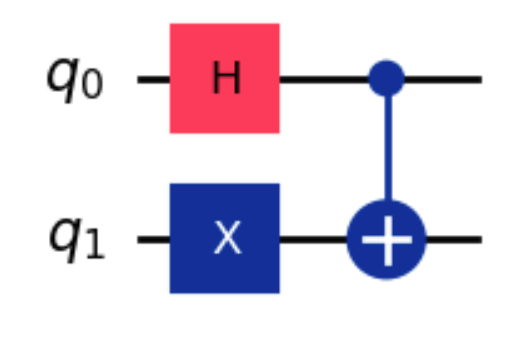
You can use tools like IBM's Qiskit framework to simulate these circuits and observe how qubits behave under different gate operations, including superposition, entanglement, and interference. I used Qiskit to simulate the circuit, and I found it pretty easy to get hands-on with it. Qiskit also provides 10 minutes of free credit to run your circuit on a real quantum computer, allowing you to experience bit of how actual quantum hardware functions.
There are many fascinating concepts to explore in quantum computing. For instance, I became interested in quantum teleportation and ended up creating a circuit to simulate it. The more you dive into it, the more intriguing and powerful these concepts become. Whether it’s building more complex circuits or exploring advanced quantum phenomena, the possibilities are endless, and the journey is just as exciting as the destination. Quantum computing truly opens the door to a whole new world of computation!
