This is a Plain English Papers summary of a research paper called Language Models: New Economic Metric Reveals True Cost & Value. If you like these kinds of analysis, you should join AImodels.fyi or follow us on Twitter.
Introduction: The Economic Challenge of Language Models
For AI systems to achieve widespread adoption, they must deliver economic value that exceeds their inference costs. This tradeoff between capabilities and costs requires metrics that account for both performance and economic efficiency. Traditional evaluation approaches that focus solely on accuracy fail to provide a complete picture of a model's practical value.
Drawing from economic production theory, researchers have developed a framework for evaluating language models that integrates performance with cost. This approach conceptualizes language models as stochastic producers - entities that convert inputs (tokens, compute) into outputs (correct solutions) with varying probabilities of success.
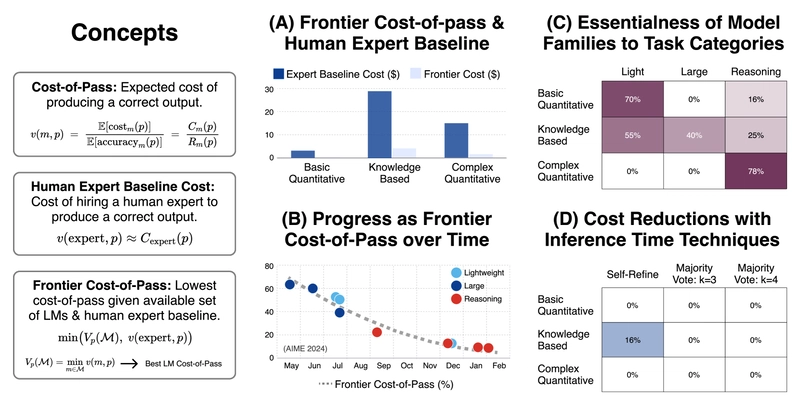
Highlights of the cost-of-pass framework and empirical analyses showing the human expert baseline comparison, frontier cost reduction over time, model family contributions, and economic benefits of inference techniques.
The researchers introduce "cost-of-pass" as their core metric - the expected monetary cost required to obtain a correct solution. This approach reveals distinct economic niches across model families, tracks progress over time, identifies which innovations drive cost efficiency, and evaluates whether common inference-time techniques provide genuine economic value.
The economic implications of language model selection extend beyond theoretical interest to practical deployment decisions that affect business outcomes and the broader economy.
Framework Foundation: Economic Theory of Production Efficiency
Classical production theory examines how producers efficiently convert inputs into outputs. Given a set of producers, this theory identifies the maximum output attainable for a given combination of inputs. The input requirement set contains all input vectors capable of producing at least a certain amount of output.
Based on this input requirement and the price of inputs, the frontier cost for producing output represents the minimum cost required. This quantifies the lowest possible cost to achieve a specified output given available production technologies and input prices.
The framework adapts particularly well to language models because they function inherently as stochastic producers - for a given input, they yield desired outputs probabilistically rather than deterministically. This stochastic nature has been addressed in economic production theory since the 1970s through concepts like stochastic frontier production functions.
The researchers adapt this economic foundation to represent the minimum achievable cost for obtaining a correct solution using language models. By incorporating the inherent variability of LM outputs directly into their cost-efficiency metric, they create a framework that aligns with core production concepts and can assess the economic impact of these stochastic AI producers.
Cost-of-Pass: An Efficiency Metric for Language Models
For a specific problem p, a model m acts as a stochastic producer whose efficiency is characterized by two quantities:
- R₍ₘ₎(p) = Probability of m producing a correct answer on p
- C₍ₘ₎(p) = Expected cost of one inference attempt by m on p
In LM contexts, inputs correspond to resources like prompt and generated tokens, while input prices represent the costs per token charged by providers. The expected number of attempts to obtain the first correct solution follows a geometric distribution with mean 1/R₍ₘ₎(p), assuming independent trials.
This yields the cost-of-pass metric:
v(m,p) = C₍ₘ₎(p) / R₍ₘ₎(p)
This formula integrates both performance (R₍ₘ₎(p)) and cost (C₍ₘ₎(p)) into a single economically interpretable metric: the expected monetary cost to obtain one correct solution. When a model cannot produce a correct answer (R₍ₘ₎(p)=0), the cost-of-pass becomes infinite, appropriately signaling infeasibility.
The cost-of-pass metric mirrors classical production theory's goal of assessing the cost of achieving a specific target output. This approach provides a practical way to evaluate the economic efficiency of language models performing real-world tasks.
The LM Frontier Cost-of-Pass
While cost-of-pass evaluates a single model's efficiency, understanding the state of LM capabilities for a given problem requires assessing the collective performance of the entire LM ecosystem. The LM frontier cost-of-pass represents the minimum cost-of-pass achievable using any available LM strategy:
V₍ₚ₎(M) = min₍ₘ∈M₎ v(m,p)
This frontier quantifies the minimum expected cost to solve problem p using the most cost-effective model currently available. If no LM can solve p, the frontier cost-of-pass becomes infinite.
By identifying this frontier, researchers can track progress in the LM ecosystem, understand which models drive economic improvements, and make rational decisions about which model to deploy for specific tasks.
Grounding Evaluation with Human Expert Baselines
The LM frontier cost-of-pass reveals the best LM performance but lacks context – it doesn't show if LMs are economically advantageous compared to human labor. To address this, the researchers introduce a human-expert baseline as a reference point.
Since qualified experts typically achieve near-perfect correctness for tasks they're trained for, their cost-of-pass approximately equals their labor cost per problem:
v(expert,p) ≈ C₍ₑₓₚₑᵣₜ₎(p)
By incorporating this baseline, the framework defines the frontier cost-of-pass considering both LMs and human alternatives:
V₍ₚ₎(M∪M₀) = min(V₍ₚ₎(M), v(expert,p))
This represents the true minimum expected cost to obtain a correct solution for problem p using the best available option, whether an LM or a human. This approach ensures the frontier cost-of-pass is always finite (assuming finite human-expert cost and capability) and provides a more complete picture of economic viability.
| Dataset | Qualification Requirements | Hourly Rate | Time per Question | Est. Cost |
|---|---|---|---|---|
| AIME | Advanced high-school contest math skills |
$\$ 45-\$ 100$ | $\sim 12$ minutes | $\$ 9-\$ 20$ |
| BBQ | General familiarity with social biases | $\$ 15$ | $\sim 0.4$ minutes (24 sec) | $\$ 0.10$ |
| GPQA Dia. | Graduate-level domain expertise | $\$ 100$ | $\sim 35$ minutes | $\$ 58$ |
| GSM8K | Basic arithmetic reasoning | $\$ 33-\$ 55$ | $\sim 3.7$ minutes | $\$ 2-\$ 3.50$ |
| MATH500 | Strong competition-level problem- solving |
$\$ 35-\$ 60$ | $\sim 12$ minutes | $\$ 7-\$ 12$ |
| Two-Digit Add. | Basic numeracy | $\$ 10-\$ 20$ | $\sim 0.04$ minutes (3 sec) | $\$ 0.01-\$ 0.02$ |
Human expert cost estimations based on qualification requirements, hourly rates, time per question, and estimated cost per problem.
Measuring Progress and Economic Value
To track improvements against the best available option over time, the researchers define Mₜ as the total set of available strategies at time t, encompassing both LM strategies released up to time t and the human-expert baseline.
The frontier cost-of-pass achievable at time t is calculated as:
V₍ₚ₎(Mₜ) = min₍ₘ∈Mₜ₎ v(m,p)
As new models are released, this frontier forms a non-increasing sequence over time, tracking the reduction in the minimum cost needed to solve particular problems.
To quantify the economic impact of new developments, the researchers define gain - the reduction in frontier cost-of-pass caused by new models:
G₍ₚ₎({mₜ}, Mₜ₋₁) = V₍ₚ₎(Mₜ₋₁) - V₍ₚ₎(Mₜ₋₁ ∪ {mₜ})
A large gain value indicates a significant economic contribution in solving problem p. This concept underlies experiments analyzing the value generated by models relative to the human baseline and tracking the evolution of the overall frontier.
These measurements can be extended to problem distributions by taking expectations across problems sampled from a distribution, enabling broader analysis of economic impact across task categories.
Budget-aware evaluation of language models provides complementary perspectives on evaluating LMs under economic constraints.
Experimental Setup and Methodology
The researchers evaluated three categories of models across three types of tasks:
Model Categories:
- Lightweight models: Those with per-token costs less than $1 per million tokens (Llama-3.1-8B, GPT-4o mini, Llama-3.3-70B)
- Large models: Large general-purpose LMs (Llama-3.1-405B, Claude Sonnet-3.5, GPT-4o)
- Reasoning models: Models with special reasoning post-training (OpenAI's o1-mini, o1, and o3-mini, DeepSeek R1)
Task Categories:
- Basic quantitative tasks: Basic numerical reasoning (Two Digit Addition, GSM8K)
- Knowledge-based tasks: Recalling and reasoning over factual knowledge (GPQA-Diamond, BBQ)
- Complex quantitative reasoning tasks: Complex mathematical reasoning (MATH-500, AIME24)
| Category | Model | Release Date | Cost (per million tokens) | |
|---|---|---|---|---|
| Input Tokens | Output Tokens | |||
| Lightweight Models | Llama-3.1-8B | 7/23/2024 | \$0.18 | \$0.18 |
| GPT-4o Mini | 7/18/2024 | \$0.15 | \$0.60 | |
| Llama-3.3-70B | 12/6/2024 | \$0.88 | \$0.88 | |
| Large Models | Llama-3.1-405B | 7/23/2024 | \$3.50 | \$3.50 |
| GPT-4o | 5/13/2024 | \$2.50 | \$10.00 | |
| Claude Sonnet-3.5 | 6/20/2024 | \$3.00 | \$15.00 | |
| Reasoning Models | OpenAI o1-mini | 9/12/2024 | \$1.10 | \$4.40 |
| OpenAI o3-mini | 1/31/2025 | \$1.10 | \$4.40 | |
| DeepSeek-R1 | 1/20/2025 | \$7.00 | \$7.00 | |
| OpenAI o1 | 12/5/2024 | \$15.00 | \$60.00 |
Per-token inference costs with release dates for each model evaluated in the study.
The evaluation methodology involved sampling up to 128 instances per dataset and running each model 8 times to estimate the expected runtime cost and accuracy per sample. This approach to efficient reasoning in large language models allows for systematic comparison across model types and task categories.
Key Findings: Model Family Economic Niches
The cost-of-pass framework reveals distinct economic niches for different model families across task categories:
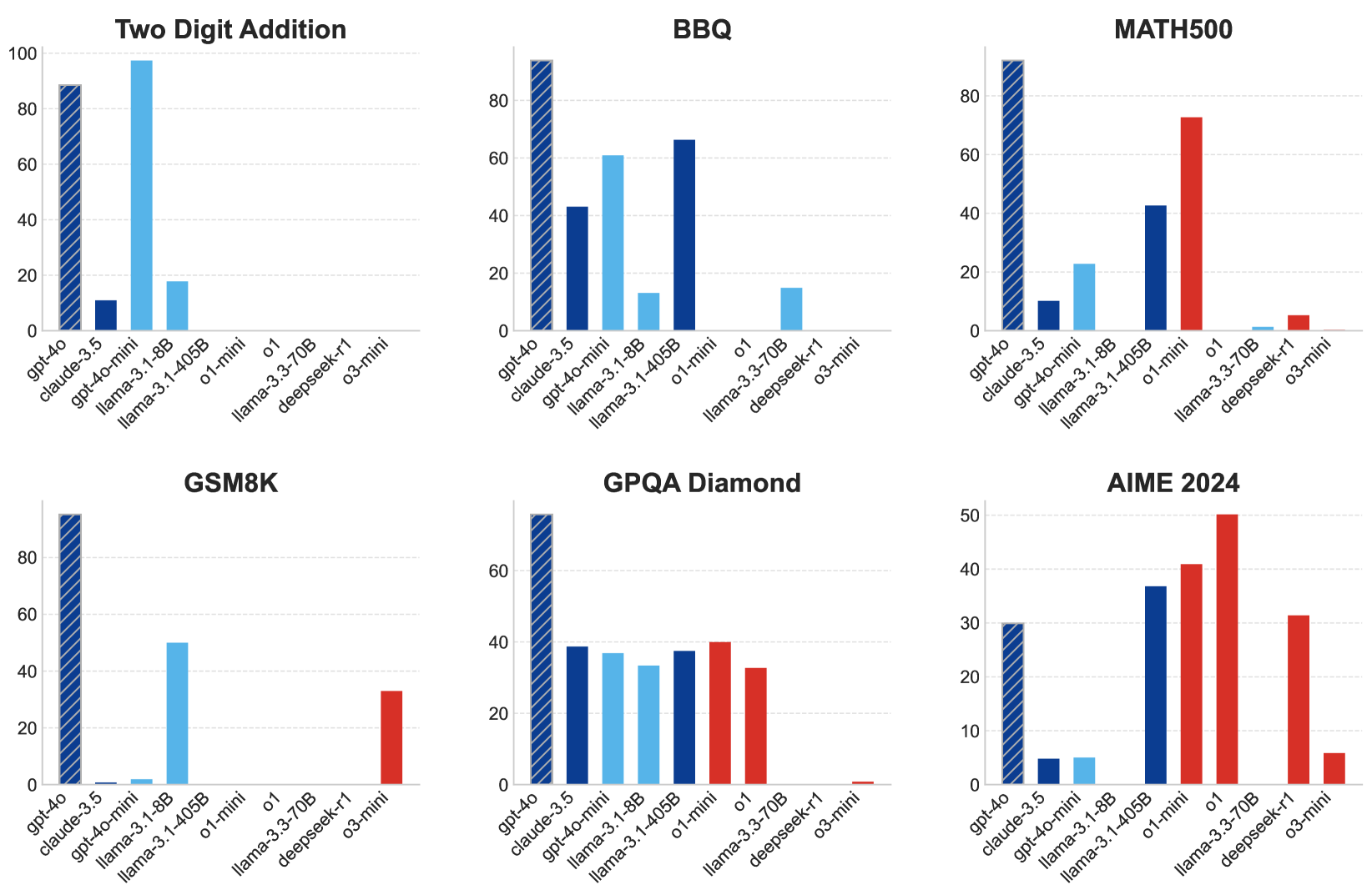
| Model Category | Basic Quantitative | Knowledge Based | Complex Quantitative | |||
|---|---|---|---|---|---|---|
| 2-Digit Add. | GSM8K | BBQ | GPQA Dia. | MATH 500 | AIME24 | |
| Lightweight Models | ||||||
| Llama-3.1-8B | $4.8 \mathrm{e}-5$ | 0.19 | $2.7 \mathrm{e}-2$ | 18.58 | 3.38 | 15.33 |
| GPT-4o mini | $5.4 \mathrm{e}-5$ | 0.22 | $1.3 \mathrm{e}-2$ | 25.38 | 2.06 | 14.67 |
| Llama-3.3-70B | $1.6 \mathrm{e}-4$ | 0.16 | $7.4 \mathrm{e}-3$ | 18.58 | 1.31 | 10.67 |
| Large Models | ||||||
| Llama-3.1-405B | $6.9 \mathrm{e}-4$ | 0.14 | $6.7 \mathrm{e}-3$ | 10.43 | 1.13 | 8.67 |
| Claude Sonnet-3.5 | $2.1 \mathrm{e}-3$ | 0.19 | $6.4 \mathrm{e}-3$ | 14.06 | 2.54 | 14.67 |
| GPT-4o | $2.3 \mathrm{e}-3$ | 0.17 | $6.2 \mathrm{e}-3$ | 14.07 | 0.96 | 14.01 |
| Reasoning Models | ||||||
| OpenAI o1-mini | $5.4 \mathrm{e}-3$ | 0.17 | $1.3 \mathrm{e}-2$ | 12.27 | 0.50 | 4.80 |
| OpenAI o1 | $1.9 \mathrm{e}-2$ | 0.22 | $4.3 \mathrm{e}-2$ | 8.07 | 0.90 | 2.85 |
| DeepSeek-R1 | $1.8 \mathrm{e}-3$ | 0.17 | $1.5 \mathrm{e}-2$ | 14.57 | 0.21 | 3.41 |
| OpenAI o3-mini | $1.1 \mathrm{e}-3$ | 0.11 | $1.1 \mathrm{e}-2$ | 8.18 | 0.76 | 2.03 |
Cost-of-pass values across different model types and tasks. Lower values (shown in blue in the original) indicate more cost-effective solutions.
The results reveal several key patterns:
Lightweight models yield the lowest frontier cost-of-pass on basic quantitative tasks. This occurs because all model families achieve high accuracy on these tasks, making the least expensive models the most cost-effective.
Large models achieve a lower frontier cost-of-pass on knowledge-based tasks compared to lightweight ones, reflecting their greater knowledge capabilities.
Reasoning models like o1, though priced significantly higher than both large and lightweight models, lead to significant performance improvements that result in lower overall cost-of-pass for complex quantitative tasks.
When evaluating models solely on accuracy or cost individually, the results favor either reasoning models (highest accuracy) or lightweight models (lowest cost) respectively. The cost-of-pass metric provides a more nuanced view by balancing these factors into a single economic measure.
This finding aligns with approaches to planning and reasoning in language models that examine the tradeoffs between different model capabilities.
Tracking Progress: The Exponential Decrease in Frontier Cost
The researchers tracked improvements in frontier cost-of-pass over time, revealing steady progress across all task categories.
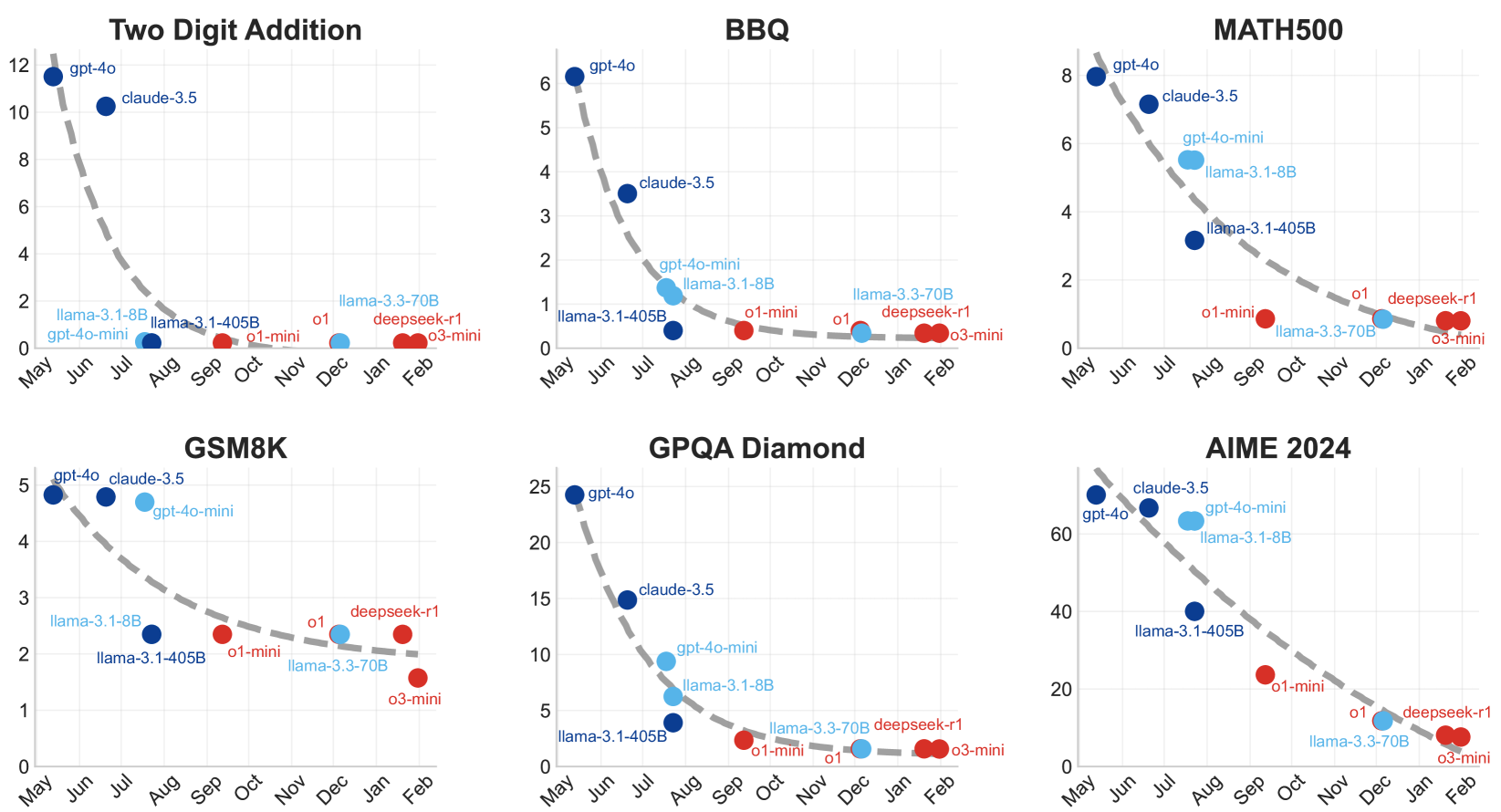
Visualization of how frontier cost-of-pass decreases over time with new model releases between May 2024 and February 2025, normalized as a percentage of the human expert baseline cost.
The results show distinct patterns across task categories:
For complex quantitative tasks, there's a consistent decline in frontier cost-of-pass over the entire period.
For knowledge-based and basic quantitative tasks, there's typically a sharp initial drop with early model releases, followed by a plateau.
By fitting an exponential decay curve to quantify these trends, the researchers found that for complex quantitative tasks between May 2024 and February 2025, the frontier cost-of-pass for MATH500 halved approximately every 2.6 months. For AIME 2024, the halving time was 7.1 months. These findings indicate consistent and substantial cost reductions over the observed period.
Bar plot showing the percentage improvement in frontier cost-of-pass contributed by each model release across different task categories.
Essential Model Families: Counterfactual Analysis
To understand which model families contributed most to progress, the researchers conducted a counterfactual analysis that quantified the impact of removing each family from the ecosystem. This involved calculating the relative improvement in frontier cost-of-pass attributable to including each model family:
G₍ₚ∼D₎(M₍ₘ₎, M₍T₎\M₍ₘ₎) / V₍ₚ∼D₎(M₍T₎)
Where M₍ₘ₎ is a family of models (lightweight, large, or reasoning), and M₍T₎ includes all models used in the experiments.
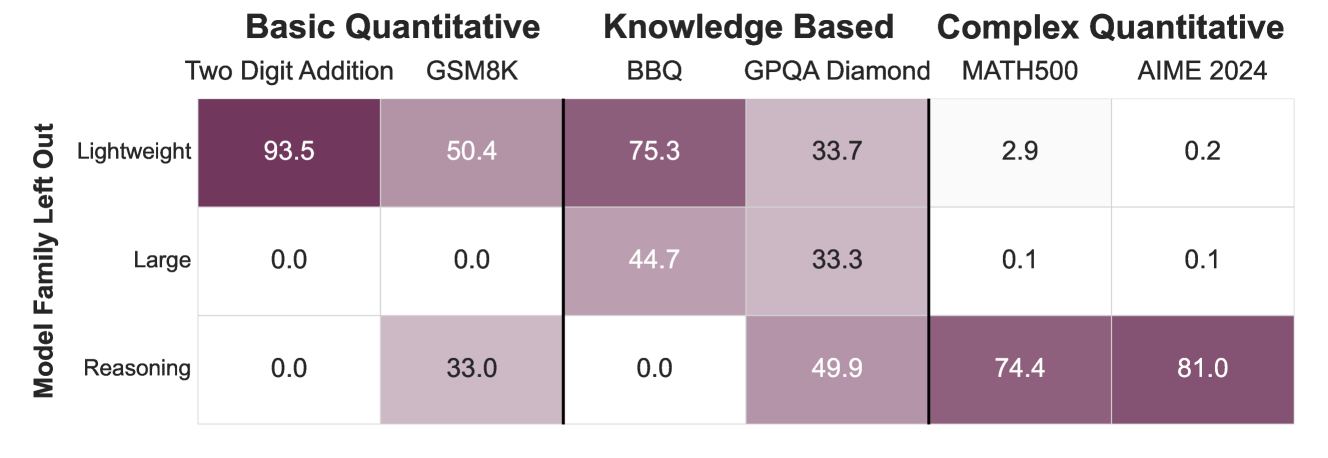
Visualization showing how much each model family contributes to improving the frontier cost-of-pass across different task categories. Higher percentages indicate greater importance to the current frontier.
The analysis revealed distinct roles across model families:
- Lightweight models help reduce the frontier cost-of-pass on basic quantitative tasks.
- Large models drive performance on knowledge-intensive tasks.
- Reasoning models play a key role in advancing the frontier for complex quantitative reasoning and also improve performance on GPQA-Diamond and GSM8K.
These findings support the observation that progress on different task types is driven by different model paradigms. Recent improvements in cost-efficiency—especially in more quantitative domains—appear largely driven by advances in lightweight and reasoning models.
The cost-of-pass framework thus provides insight into which model innovations matter most for economic efficiency across different application domains.
Inference-Time Techniques: Limited Economic Benefits
The researchers assessed whether common inference-time techniques provide meaningful economic benefits compared to baseline model performance. They measured the relative improvement in frontier cost-of-pass when applying techniques uniformly across models:
G₍ₚ∼D₎(M₍L₎*, M₍L₎) / V₍ₚ∼D₎(M₍L₎)
Where M₍L₎ represents the set of lightweight and large models, and M₍L₎* represents the same set with an inference-time technique applied.
| Inference Time Technique | Basic Quantitative | Knowledge Based | Complex Quantitative | ||||
|---|---|---|---|---|---|---|---|
| Two Digit Addition | GSM8K | BBQ | GPQA Diamond | MATH500 | AIME24 | ||
| Self-Refine | 0 | 0 | $\mathbf{6 . 7}$ | $\mathbf{2 4 . 9}$ | 0 | 0 | |
| Maj. Vote $(\mathrm{k}=3)$ | 0 | 0 | 0 | 0 | 0 | 0 | |
| Maj. Vote $(\mathrm{k}=4)$ | 0 | 0 | 0 | 0 | 0 | 0 |
Relative performance gains (%) from different inference time techniques across datasets. Bold values indicate where meaningful improvements were observed.
The findings show:
Self-refinement shows moderate economic benefit on knowledge-intensive tasks, with a notable 24.9% improvement on GPQA Diamond.
Majority voting (with 3 or 4 votes), despite potentially enhancing raw accuracy, does not offer relative economic improvement across any of the tested datasets.
These results suggest that for the evaluated techniques, the increased computational costs typically outweigh the performance benefits relative to the frontier cost-of-pass established by the baseline models. This implies that common inference-time approaches may not yield significant economic benefits on their own.
The findings underscore that direct model-level innovations appear to be the primary drivers of cost-efficiency, rather than inference-time techniques.
Conclusion: Implications for the AI Economy
The economic framework presented in this research offers a principled approach to evaluating language models by integrating performance and inference cost. By conceptualizing language models as stochastic producers, the cost-of-pass metric provides an economically interpretable measure of efficiency.
The analysis reveals several key insights about the language model ecosystem:
Distinct economic niches exist across model families: lightweight models excel at basic tasks, large models at knowledge tasks, and reasoning models at complex problem-solving.
Progress is rapid and measurable: The frontier cost-of-pass has declined exponentially, with complex quantitative tasks seeing costs halve every few months.
Complementary innovations drive progress: Different model families push the frontier in different task categories, highlighting the importance of diverse approaches.
Inference-time techniques provide limited value: Common techniques like majority voting and self-refinement rarely justify their added costs compared to model-level improvements.
These findings have significant implications for AI development and deployment. They suggest that focusing on model-level innovations that improve the cost-efficiency frontier will yield greater economic benefits than optimizing inference techniques. The framework also provides a principled tool for guiding model selection based on the economic value delivered for specific applications.
As language models continue to evolve, this economic perspective offers valuable guidance for researchers, developers, and organizations seeking to leverage AI capabilities effectively while managing costs. By measuring progress in terms that directly reflect economic value, the framework helps align AI development with practical real-world considerations.