🎯 Juggling Algorithm: Rotate Arrays Like a Pro! 🔄✨

Hey there, coding wizard! 👋 Ever wondered how to rotate an array in place without using extra space? Let’s dive into the Juggling Algorithm, a clever and efficient technique that uses modular arithmetic and cycles to rotate arrays with minimal effort. By the end of this post, you'll be ready to tackle any array rotation problem like a pro! 🚀

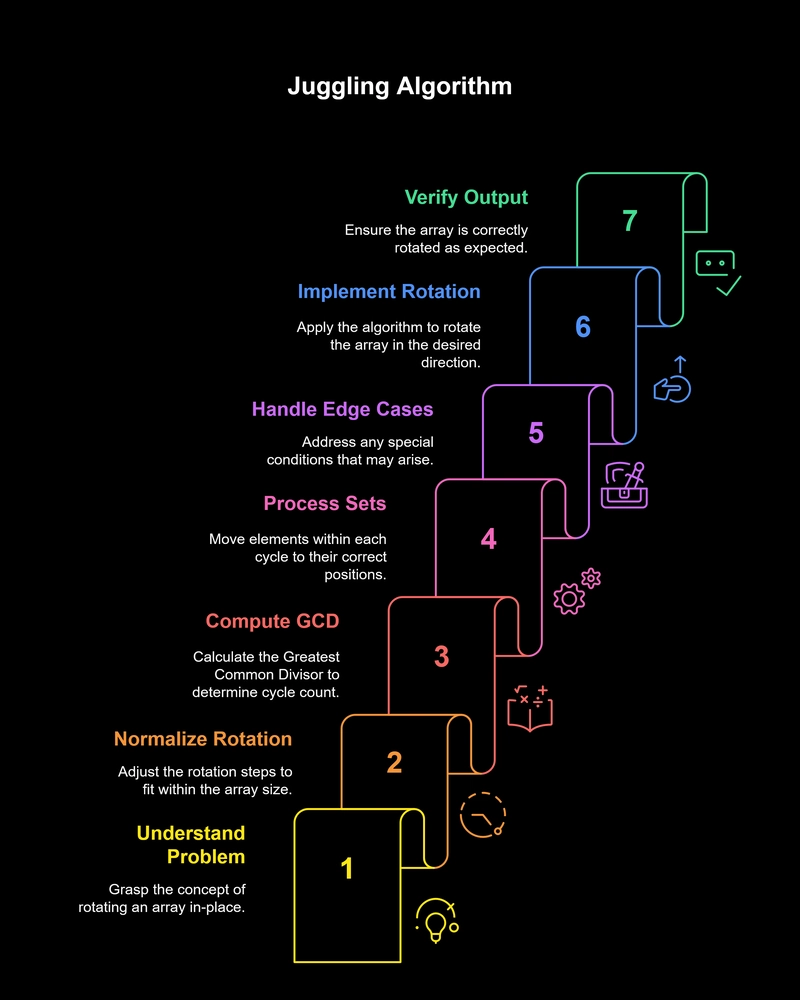
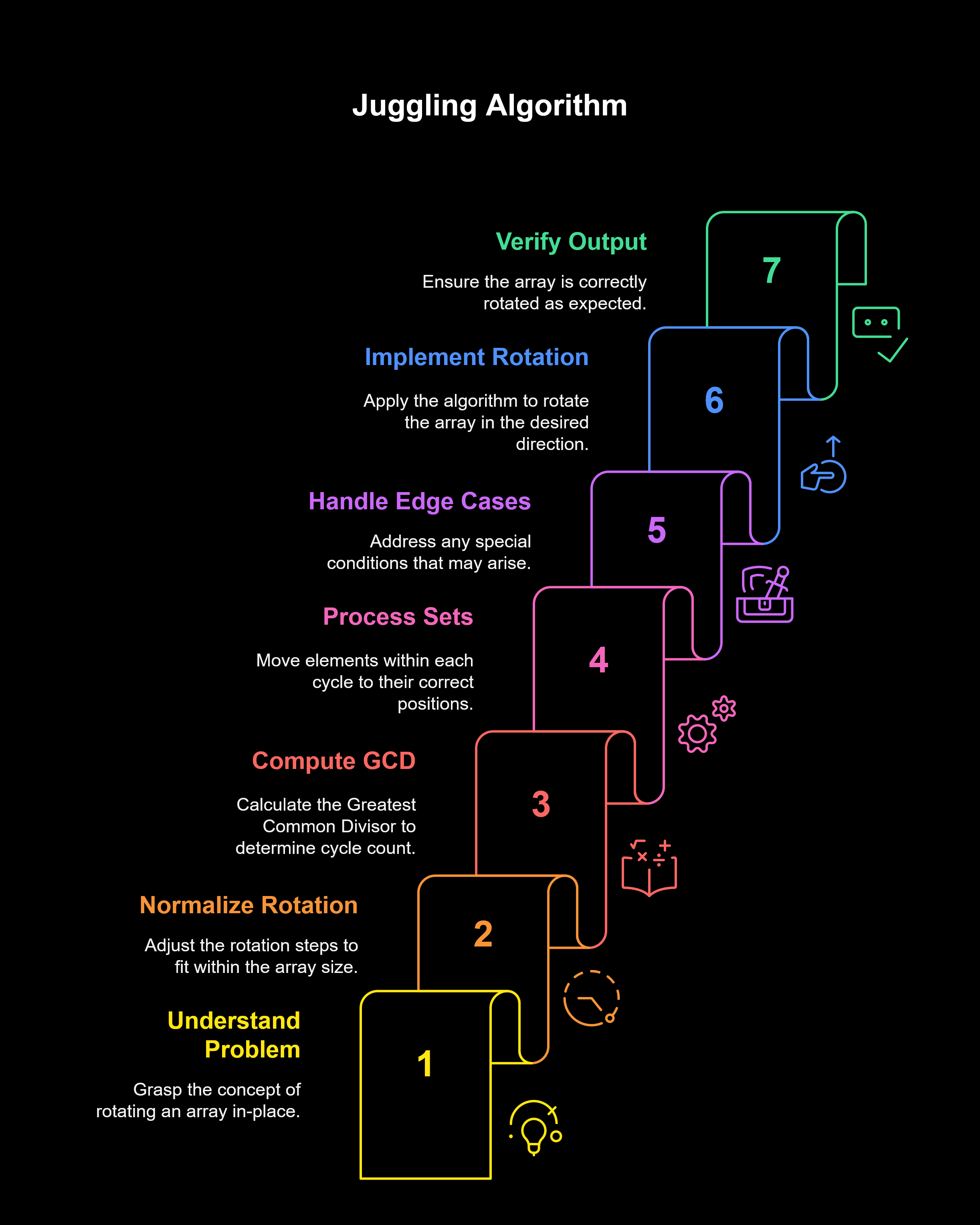
What is the Juggling Algorithm?

The Juggling Algorithm is an elegant solution for rotating an array to the left (or right) by d steps. It works by dividing the array into cycles based on the greatest common divisor (GCD) of the array length n and the number of rotations d. Each cycle contains elements that need to be rotated among themselves, making the process both intuitive and efficient.

How Does the Logic Work?

  1. Adjust d:

    If d > n, we only need to rotate by d % n steps because rotating the array by its length brings it back to its original state.

  2. Find GCD:

    The number of cycles required is determined by the GCD of n and d. For example, if n = 6 and d = 2, the GCD is 2, so the array will have 2 cycles.

  3. Rotate Each Cycle:

    • Start from the first element of each cycle.
    • Move elements in steps of d until you return to the starting position.
    • Use a temporary variable to hold the first element of the cycle and place it at the correct position at the end.

Logic : Flow Chart

Juggle Algo

Interactive Example: How It Works

Let’s walk through an example step-by-step:

Input: 

arr = [1, 2, 3, 4, 5, 6]
d = 2

Step 1: Adjust d

Since d < n, no adjustment is needed.

Step 2: Find GCD

The GCD of n = 6 and d = 2 is 2. So, we’ll have 2 cycles.

Step 3: Rotate Each Cycle

Cycle 1 (Start at index 0):

  • Temporarily store arr[0] = 1.
  • Move arr[2] → arr[0], arr[4] → arr[2], and finally place temp → arr[4].
  • Result after Cycle 1: [3, 2, 5, 4, 1, 6].

Cycle 2 (Start at index 1):

  • Temporarily store arr[1] = 2.
  • Move arr[3] → arr[1], arr[5] → arr[3], and finally place temp → arr[5].
  • Final result: [3, 4, 5, 6, 1, 2].

Time and Space Complexity

Time Complexity:

  • Calculating the GCD takes O(log(min(n, d))).
  • Rotating all elements takes O(n) since each element is moved exactly once.
  • Overall Time Complexity: O(n) 🚀

Space Complexity:

  • The algorithm uses only a few variables (temp, current, etc.), so it operates in O(1) space.

Why Should You Care?

The Juggling Algorithm is a perfect blend of simplicity and efficiency. Whether you’re preparing for technical interviews 💼 or solving real-world problems, this algorithm is a must-know. Plus, it’s a great way to impress your peers with your coding skills! 😎

Key Takeaways

  • The Juggling Algorithm divides the array into cycles based on the GCD of n and d.
  • It rotates arrays in O(n) time and O(1) space, making it highly efficient.
  • Understanding this algorithm will boost your problem-solving skills and prepare you for challenging coding tasks.

So, what are you waiting for? Grab your keyboard and start juggling arrays today! 🤹‍♂️✨

#Algorithms #Coding #DataStructures #TechTips #ProblemSolving