Hey folks! This is one of those posts I was really excited to write: we're finally talking about math! Yes, the one that many people try to run from... but in the world of gamedev, it can become one of our greatest allies.
I’ve always loved this subject, especially because it blends perfectly with game development -- especially when the goal is to add that visual spice that transforms a prototype into something that feels like a game.
Those little effects that make everything look smoother, more dynamic, more alive. That famous magic of game feel (you’ll see me talk a lot more about that in future posts 😄).

🧠 Math Is Everywhere
Math is like the invisible engine behind almost everything that works in a game (in world, actually!). From basic movement to physics and particle systems -- there’s always some formula running under the hood.
And when it comes to bringing systems and movement to life in games, one branch of math really stands out: trigonometry.

🔺 The Unit Circle (Wait, don’t run!)
For many, trigonometry is that horrible topic from high school that caused some sleepless nights. But believe me -- in the right context, it’s actually fun and extremely useful.
It all starts with the unit (or trigonometric) circle: a representation of a circle where each point on the edge can be described by an angle. That angle gives us two magical values: sine (sin) and cosine (cos). These basically tell us the height and width of a point on the circumference.
In the next image, take a look at sin behaviour:
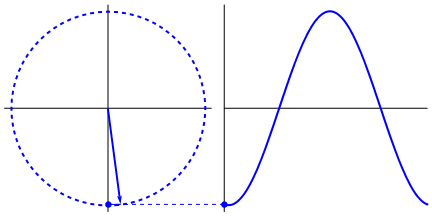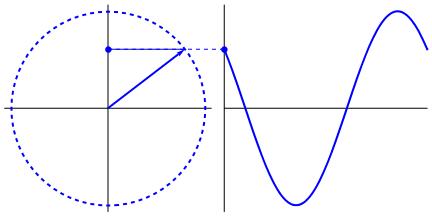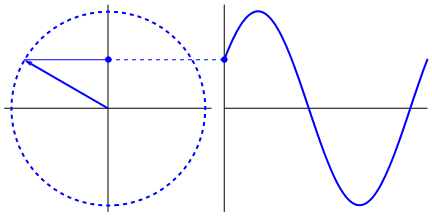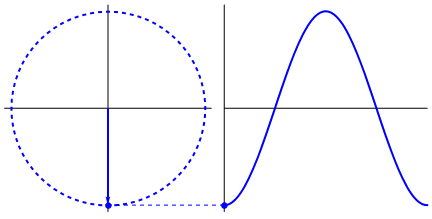
If we try to get the sine of any value -- for example, the game’s running time -- we get the projection of that angle from -1 to 1. This creates a sine wave, an awesome and easy ripple effect.
These functions are cyclical -- they repeat -- and that makes them perfect for simulating smooth, continuous patterns in games.

✨ Trigonometry in Visual Effects
Sure, trig includes tangents, secants, cotangents... but let’s keep it simple. Here, we’ll stick to sine and cosine -- they’re more than enough to create some really cool stuff.
Here some examples:
🔸Circular movement: enemies orbiting the player, or spinning items on the map.
🔸Subtle pulses: like that "breathing" effect on menu buttons.
🔸Oscillations: sprites floating or gently swaying.
🔸Arcing projectiles: like arrows or magical spells.
🔸Rotating lasers: using dynamic angles.
🔸Waves and tremors: screen shake or shader effects.
🔸Wobbly stuff: that jiggly, gooey motion like a slime creature or melting object.
All of this can be done with just a few lines of code using sine, cosine, and time.

🎮 Trigonometry in Game Logic
Modern engines come with tons of features built-in -- from collision detection to movement using vectors. But knowing a bit of math gives you more freedom and flexibility to do things your way.
For instance, instead of using a bunch of ifs to determine which direction sprite to show based on player movement, you can just compare the sine and cosine values of the movement angle. Something like:

That famous quote comes to mind: “It looks like magic, but it’s just math.”
📈 The Learning Curve
It seems complicated at first -- and that’s totally normal. Years ago, I used to avoid anything that involved sine or cosine in my projects. I thought, "That stuff isn’t for me."
But then came our old friend: the Megaman Method™.🔵⚙️
Every challenge we overcome gives us a new weapon, a new skill. At first, we get wrecked. But after repeating a few levels and defeating some bosses, we realize we’ve leveled up. And before we know it... we’re using sin(time) to animate our HUD energy bar 😅

What used to be scary becomes fun. And every new technique is one more power added to our arsenal.
💡 EXTRA: Trig Fun Facts
🔢 atan2(y, x) is a hero: this function calculates the correct angle of a vector on a Cartesian plane, accounting for all quadrants. It’s used to aim enemies toward the player, create auto-aiming systems, or just figure out where something’s heading.
🔫 Bullet Hell games: Games with crazy projectile patterns (like Archvale or Enter the Gungeon) use trig all the time! Patterns follow rules like angle + sin(time) or angle += speed, creating hypnotic and challenging effects.
🎨 Advanced shaders: In shaders, just sine and cosine can go a long way. You can create real-time waves, distort textures, make psychedelic effects... it’s the ultimate playground (for the brave-hearted) of trigonometry.
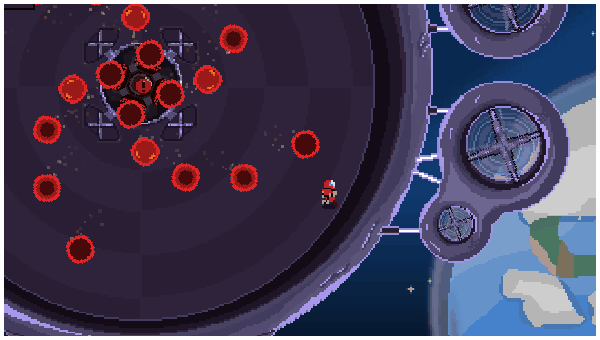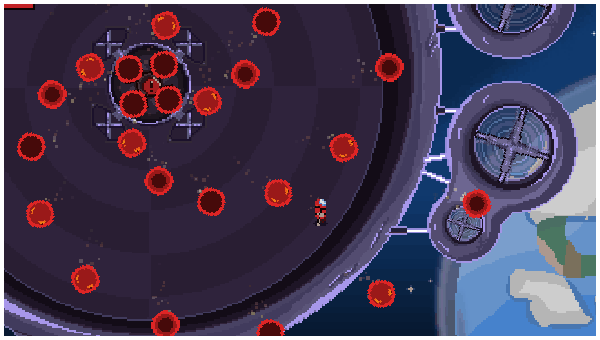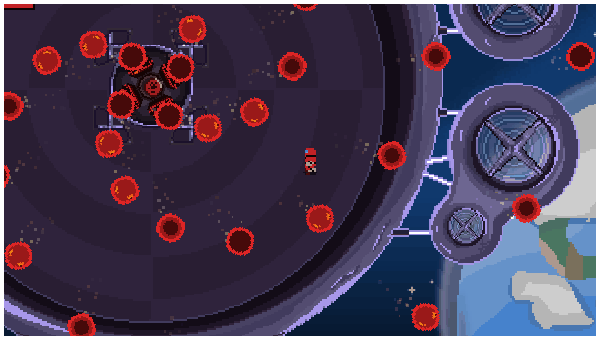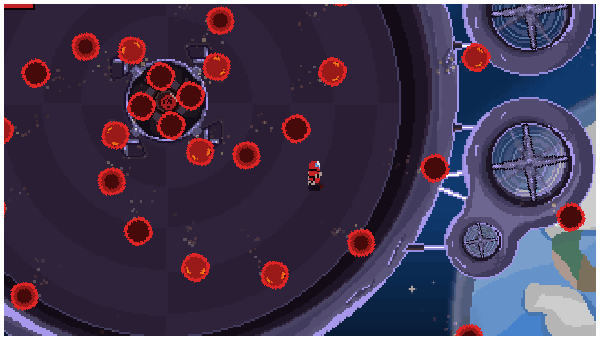
🚀 To Wrap It Up...
You don’t need to master every bit of math to make amazing games. But the more you explore it, the more doors open -- and the more magical your creations become.

So if you’ve made it this far, why not try sprinkling a little sine and cosine into your next project? Whether it’s for a visual touch or an elegant solution to a complex logic -- math might just become your best sidekick.
Make math your ally -- and I promise: this knowledge will transform your projects.

Trust the Megaman Method™.

