งานนี้เราจะศึกษาเรื่อง Similarity ที่เป็นพื้นฐานสำคัญของ Unsupervised learning โดยเฉพาะการจัดกลุ่มข้อมูล หรือการหา Nearest Neighbor เราจะเปรียบเทียบด้วย2วิธีประกอบไปด้วย
1.Euclidean Distance: วัดระยะเส้นตรง (แบบเส้นตรงระหว่างจุด A ถึง B)
2.Manhattan Distance: วัดระยะทางแบบเดินเป็นเส้นตรงตามแนวแกน (คล้ายการเดินในเมืองแมนฮัตตัน)
หลักการของโค้ดที่เกี่ยวกับ Euclidean Distance และ Manhattan Distance




ผลก็คือ
ค่า Euclidean < Manhattan เสมอ เพราะ Euclidean คือ “ทางลัดตรง” ในขณะที่ Manhattan คือ “ทางอ้อม”
https://colab.research.google.com/drive/1p0IYRxBPyTR5jWrD1MlPNbVKrxQ3ON8j?usp=sharing
เรามาดูตัวอย่างแอปที่ใช้งาน Euclidean และ Manhattan กันดีกว่า
1.K-Nearest Neighbor (KNN) ส่วนใหญ่ใช้ Euclidean วัดความใกล้ของเพื่อนบ้าน
2.Clustering (k-Means) ใช้Euclidean เป็นหลัก ใช้ในการจัดกลุ่มด้วย centroid
3.Outlier Detection Manhattan มักเสถียรกว่า ทนต่อค่าที่โดดเด่น (extreme)
ตัวอย่างการใช้งาน Euclidean และ Manhattan ในการคำนวณและใช้งานจริง
เป้างานของงานโค้ดนี้คือ ห้างสรรพสินค้าแห่งหนึ่ง ต้องการหาลูกค้าที่ “มีลักษณะใกล้เคียงกับลูกค้าเป้าหมาย” เพื่อเสนอโปรโมชั่นที่เหมาะสม โดยจะวัดด้วย ความใกล้เคียงจาก รายได้ต่อปี (k$) และ คะแนนการจับจ่าย (1-100) และใช้ Euclidean และ Manhattan distance เพื่อวัดว่าใครใกล้ที่สุดกับลูกค้าเป้าหมาย
ข้อมูลตัวอย่างลูกค้า

โค้ดการรันและผลที่ได้
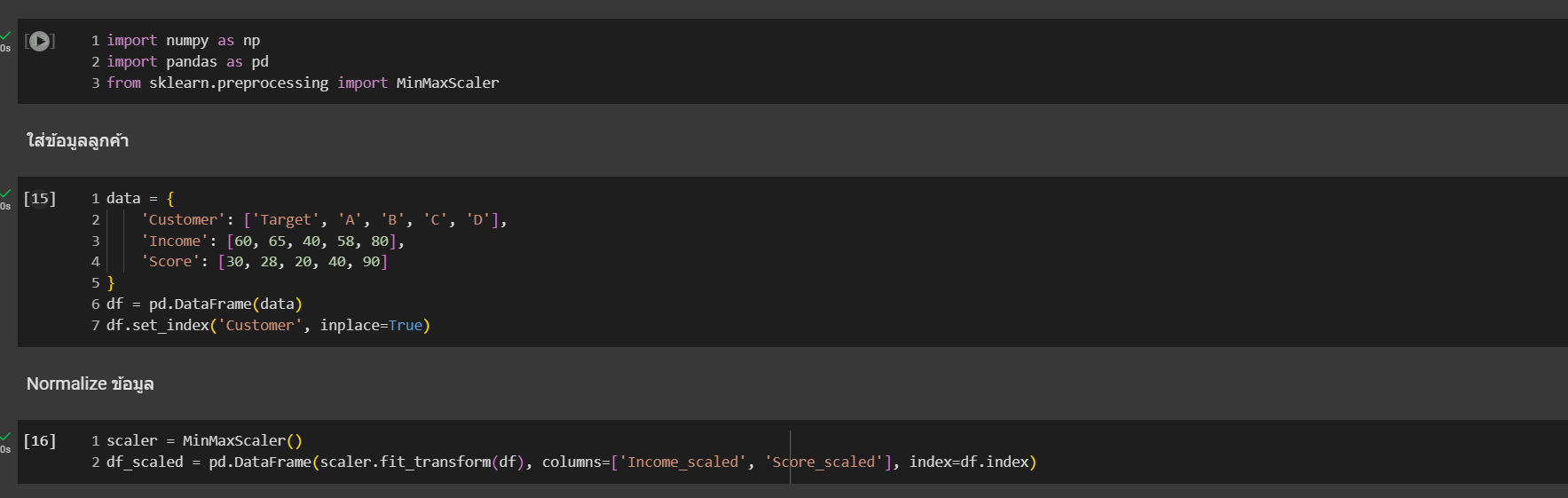
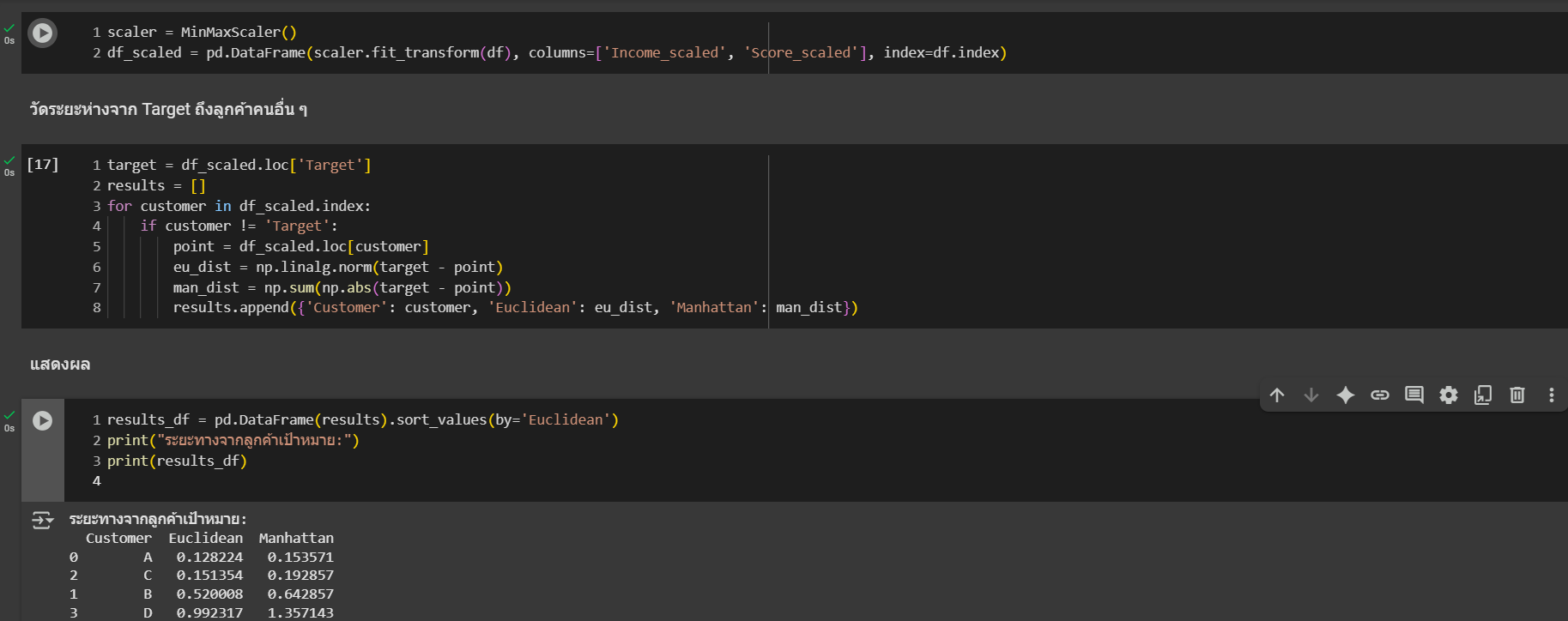
https://colab.research.google.com/drive/1p0IYRxBPyTR5jWrD1MlPNbVKrxQ3ON8j?usp=sharing
จากผลที่ได้
ลูกค้า A มีระยะทางต่ำที่สุด ทั้ง Euclidean และ Manhattan เป็นกลุ่มที่ใกล้ที่สุดกับเป้าหมาย
ลูกค้า D มีระยะมากที่สุดและไม่ควรเลือกให้รับโปรเดียวกัน
ถ้าใช้ Manhattan Distance จะเห็นผลคล้ายกัน แต่อาจสลับลำดับในบางกรณี
หากข้อมูลมี outlier หรือความเบี่ยงเบนสูงมาก Manhattan จะมีประสิทธิภาพที่กว่า
ในทางกลับกัน ถ้าค่าทุกมิติคงที่และมีการ normalize แล้ว Euclidean ให้ผลดีและเร็ว
สรุปเนื้อหา
ทั้ง Euclidean และ Manhattan ใช้ในการวัดความคล้ายกันของข้อมูลแต่เมื่อค่ามีความคงที่ จะเกิดความแตกต่างของทั้ง2ตัว
ตัวของEuclidean เหมาะกับกรณีที่ทุก feature มี scale เท่ากันและไม่มี outlier มาก
ตัวของManhattan เหมาะกับข้อมูลที่มีค่า outlier เพราะไม่ยกกำลัง
แต่ยังไงการที่เรา normalize ข้อมูลก่อนก็ย่อมดีกว่าเพราะจะทำให้เราได้ทั้งไทป์ของข้อมูลและการเลือกใช้งานให้ถูกต้อง และเรายังสามารถนำงานเหล่านี้ไปใช้กับงานที่คล้ายๆกับที่ยกตัวอย่างได้
สุดท้าย บทความนี้เขียนมาเพื่อให้เห็นภาพว่า การเลือกวิธีวัดระยะทางที่เหมาะสม ไม่เพียงแต่จะช่วยให้โมเดล AI ทำงานได้ดีขึ้น แต่ยังส่งผลโดยตรงต่อความแม่นยำและประสิทธิภาพของการตัดสินใจอีกด้วย โดยเฉพาะเมื่อข้อมูลมีความหลากหลายหรือมีลักษณะเบี่ยงเบนสูง การเลือกใช้ Manhattan Distance อาจให้ผลลัพธ์ที่เสถียรกว่า ขณะที่ Euclidean เหมาะกับข้อมูลที่ผ่านการปรับสมดุลมาแล้วและต้องการวัดความใกล้ชิดแบบเส้นตรงที่แม่นยำ.