In relational databases like MySQL, indexes are the foundation of efficient data retrieval. Among various indexing strategies, composite indexes — those spanning multiple columns — offer significant performance advantages when dealing with complex queries.
This article takes a deep dive into the structure of composite indexes in MySQL, their search behavior, and the rationale behind the leftmost prefix rule.
Composite Index Storage Structure
As we’ve discussed earlier, let’s now refer to a previously mentioned Q&A example to explore today’s topic: the storage structure of composite indexes.
In a user-submitted question about composite index storage structure, someone gave the following answer:
Table T1: (a int primary key, b int, c int, d int, e varchar(20))
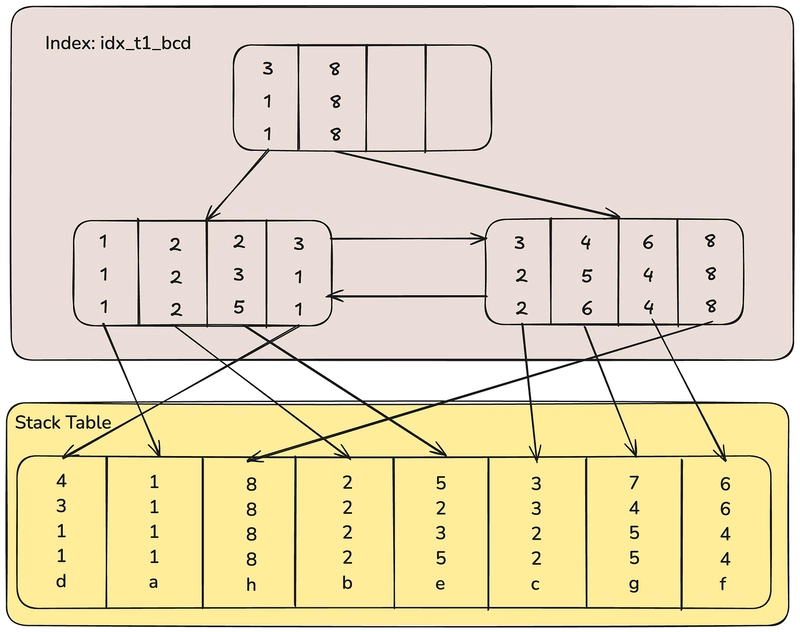
create index idx_t1_bcd on t1(b,c,d);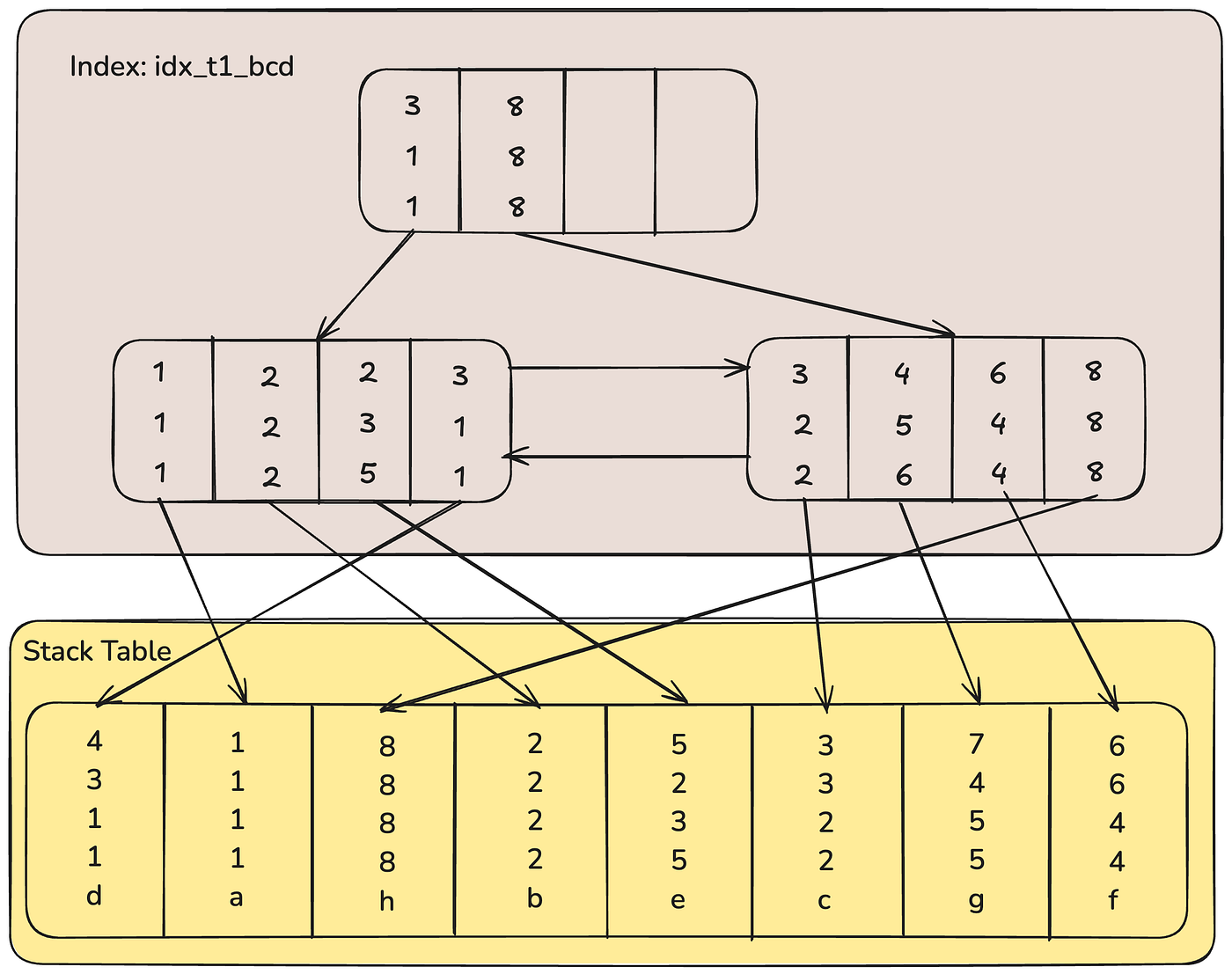
A composite index on
*b, c, d*looks like this in the index tree. During comparison,*b*is checked first, followed by*c*, and then*d*.
Since the answer only includes a single image and a brief sentence, it might be a bit hard to understand at a glance.
So, let’s build upon this earlier explanation and use that example to dive deeper into how composite indexes are stored in a B+ tree.
Let’s begin with the table T1, which has the columns a, b, c, d, and e.
Here, a is the primary key. Except for e, which is of type VARCHAR, the other columns are of type INT. A composite index idx_t1_bcd(b, c, d) has been created on this table.
Since the image shown earlier used only two tree levels, which can be difficult to grasp, we’ll now use some hypothetical table data and show a refined illustration of the composite index structure in a B+ tree.
Note: This example is based on the InnoDB storage engine.
Suppose the T1 table contains the following data:
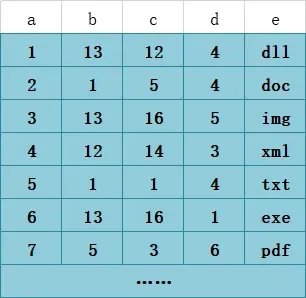
Then, based on the composite index (b, c, d), the B+ tree would roughly look like the diagram below. (For example, take the first entry of the root node: 1 1 4, which corresponds to b = 1, c = 1, d = 4.)
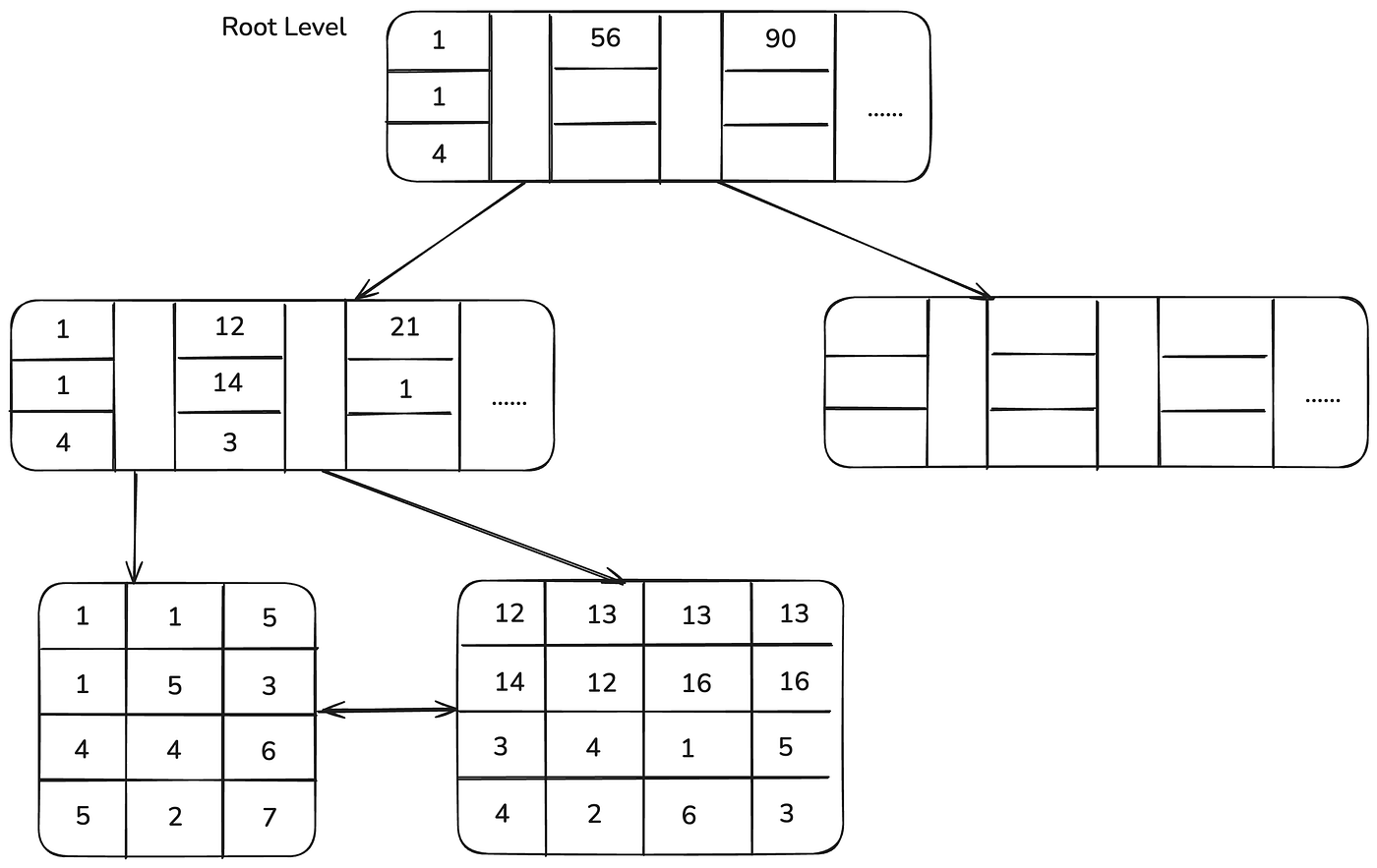
Through these two diagrams, we should now have a rough understanding in our minds of the storage structure of composite indexes on a B+ tree.
Let’s first look at table T1. For its primary key a, let’s temporarily assume it is an integer and auto-incremented (PS: as to why it's an integer and auto-incremented, the previous two articles have detailed explanations, so we won't repeat them here). InnoDB uses the primary key index to maintain both the index and the data file via a B+ tree. Then, when we create a composite index on (b, c, d), it also generates an index tree, which is likewise a B+ tree structure. However, the data part of its leaf nodes stores the primary key value of the row where the composite index resides (as shown in the diagram with the purple background in the leaf nodes). As for why the data part of a secondary index stores the primary key value, that was also discussed in the previous article — if you're interested or haven’t read it yet, feel free to take a look.
Alright, now that we’ve covered the general situation, let’s use these two diagrams to explain a few points.
Compared with a single-column index, a composite index just contains several more columns, and all of those indexed columns appear in the index tree. For a composite index, the storage engine will first sort based on the first indexed column. As shown in the diagram, let’s look at the last layer of the B+ tree — if we only look at the first indexed column in the leaf nodes (i.e., the first row), the values are 1, 1, 5, 12, 13, 13, 13, which are clearly in ascending order. That is: if the first column’s values are equal, then sorting is done by the second column, and so on — this is how the index tree shown above is built.
Moreover, if we look at the second and third rows, which represent the c and d columns of the composite index, their values are respectively:
1, 5, 3, 14, 12, 16, 16 (for c) and
4, 4, 6, 3, 4, 1, 5 (for d).
Here, you can see that these rows are no longer in strictly increasing order. However, when values in the **b** column are equal, the values in the c column tend to be increasing — for example, when b = 1, we have 1, 5; when b = 13, we have 12, 16, 16. Similarly, when values in the **c** column are equal, the d column values will tend to be increasing. This is precisely why we must follow the Leftmost Prefix Principle.
Summary
Multi-column key organization based on B+ tree
A composite index combines multiple fields into a single key value and builds a B+ tree according to the order in which the fields are defined. For example, for a composite index (b, c, d), each node's key values are arranged in the order b → c → d.
-
Non-leaf nodes: Store the full composite key values (like combinations of
b, c, d) and pointers to child nodes. -
Leaf nodes: Store the complete composite index key values (
b, c, d) and the corresponding primary key value (used for table lookups).
Sorting rules
-
Global order: All nodes are ordered by the first (leftmost) column; if the first column’s values are equal, the second column is used, and so on. For example,
(b=1, c=2)comes before(b=1, c=3). - Local order: Within the same level, the key values stored in each node are ordered, which supports efficient range queries.
Physical storage optimization
- Non-leaf nodes in a B+ tree do not store actual data; they only store key values and pointers. This allows each disk page (e.g., 16KB) to hold more key values, reducing the height of the tree (usually 3–4 levels are enough to support tens of millions of rows).
- Leaf nodes are connected via doubly linked lists, making range scans efficient.
Leveraging AI for SQL Optimization
In the realm of database optimization, tools like Chat2DB are emerging to assist developers in refining their SQL queries. Chat2DB utilizes AI to analyze SQL statements and suggest improvements, such as optimal index usage or query restructuring. While it’s not a replacement for in-depth knowledge of database internals, it serves as a valuable aid in identifying potential performance enhancements.
Community
Go to Chat2DB website
🙋 Join the Chat2DB Community
🐦 Follow us on X
📝 Find us on Discord