Understanding RSA - The Math behind modern encryption

As developers we often come across different encryption algorithms like MD5, AES, DES and so on, however RSA stands out because it is simple yet significant or should I say 'fascinating', so enough chit chats let us dive into how RSA actually works.

How Does RSA work ?

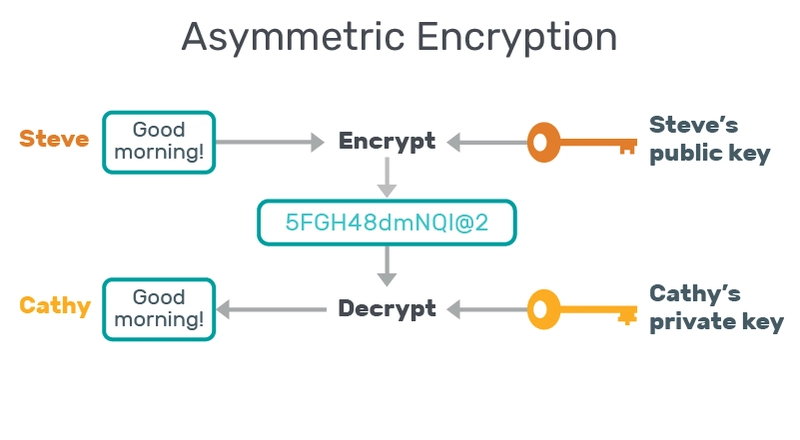
RSA is an asymmetric encryption algorithm that uses mainly 2 types of keys (public and private) to encrypt the data, the working of the RSA is quite simple, here is an example,

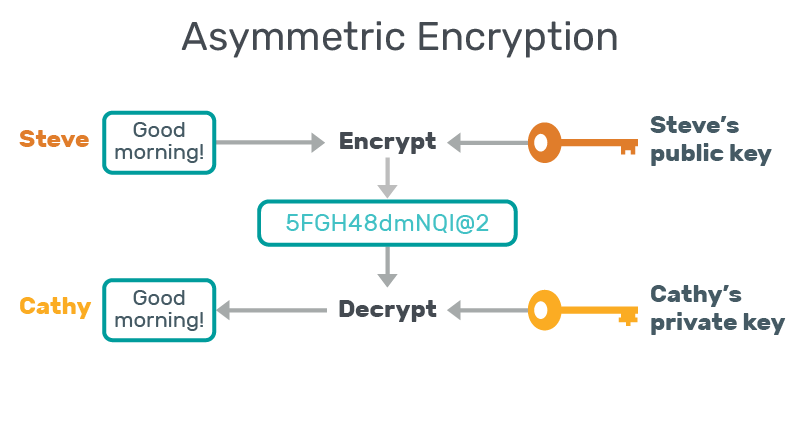
so let us assume that Steve needs to send a message to Cathy, so that message is encrypted using Steve's public key and that can only be decrypted by Cathy's private key and vice versa, this is just a vague representation of how it works, but you may think what's so fascinating about this, now let us dive deeper

Math does the magic

Ok "RSA this! RSA that! what if the keys are compromised?" might be a great question, so to answer that let us get our hands on the "Math Problem" which is used to create a public and private key pair,

we need constants such as p, q, n, e and d

step 1: Select 2 prime numbers (p and q)

• let $p = 61$ $q = 53$

step 2: Find the (n)

• $n = p * q = 3233$

step 3: find the Euler's totient $Φ(n)$

• Euler's totient can be found by:
  $$Φ(n) = (p - 1) * (q - 1)$$
  $$Φ(n) = (61 - 1) * (53 - 1) = 3120$$

step 4: Choose the public exponent e

• e can be any number that satisfies the following

1. $1 < e < Φ(n)$
2. $e$ and $Φ(n)$ are co-primes or simply $GCD(Φ(n), e)$ should be 1

• so let us assume e = 17

step 5: finding d the private exponent, the secret number

• d can be arrived by applying euclidean equation such that
  $$d \ * \ e \ mod \ Φ(n) = 1$$
• so applying this will give $d \ * \ 17 * mod \ 3120 = 1$

the above equation solves to 2753

(note: d is just the multiplicative inverse of e, to make it even simpler d is a number that 'unodoes' the effect of e)

step 6: Encryption and decryption

• now since we have all the required constants, we can see the encryption and decryption.

• let us assume that we have to encrypt a message m 65

• now let us decrypt the cipher with d
  $$message (m) = c^d \ mod \ n$$
  $$m = 2790^{2753} \ mod \ 3233$$
  $$m = 65$$

where m is our actual message
aight !! I know too much math,so to summarize

e is public exponent
d is private exponent
n is product of p and q

so our

public key is (e,n) that is (17, 3233)
private key is (d, n) that is (2753, 3233)

So how's this math problem difficult to crack ?

So here RSA relies on a principle called prime factorization, so to simply say, it is easy to find the product (n) of 2 prime numbers (p and q) but it is very difficult to find out the 2 factors that make up the number (n) so for example:

• it is easy to calculate the product of 61 and 53
• but it is difficult to say the factors of 3233 especially when the size of number n is bigger

(note: here we have taken 4 digit number but in real scenario the number would be of 4096 bits)

So this mathematical property makes RSA very difficult to crack, and the important thing to note is cracking RSA is not impossible but the computing that is needed to crack it is extremely high, even for today's standards and some studies say that the computing time that is needed to crack this problem would take even decades.

So, this is how a math problem could solve the need of extremely a strong encryption mechanism and today RSA is one of the widely used encryption algorithms out there.