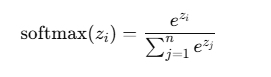Whenever we ask a neural network to make a prediction — say, to classify an image or understand the sentiment of a sentence — it doesn’t just blurt out a single answer. Instead, it gives us a distribution of probabilities across all possible classes. For example:
“I’m 85% sure this is a cat, 10% it’s a dog, and 5% it’s a rabbit.”
But how does the model arrive at these confident numbers? That’s where **Softmax **enters the scene.
And once it predicts, how do we teach the model whether it was right or wrong — and how wrong it was? That’s the job of Cross-Entropy Loss.
In this blog, we’ll break down these two foundational concepts Softmax and Cross-Entropy. Whether you’re building your first image classifier or trying to understand loss functions in deep learning, mastering this duo is essential.
What is Softmax?
Softmax is a mathematical function used in machine learning, especially in classification problems, to convert raw prediction scores (called logits) into probabilities which always add up to 1.
The input values can be any real number, but softmax transforms them into a range between 0 and 1, making them interpretable as probabilities.
📐 Formula
For a vector z= [z1,z2,....,zn], the softmax function is defined as:
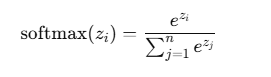
Key ideas:
- e^zi: Highlights strong preferences.
- Denominator: Ensures the outputs sum to 1.
💻 Python Implementation

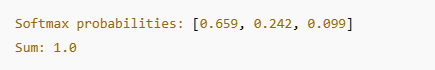
What is Cross-Entropy?
After softmax gives us probabilities, Cross-Entropy tells us how close those predictions are to the actual label.
Cross-Entropy (or log loss) is a performance metric for classification models. Lower is better, with 0 being perfect.
📐 Formula
For a true label vector 𝑦 and predicted probabilities y^:
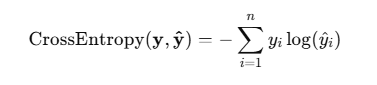
Let’s say your true label is [ 0, 1, 0 ] i.e., the correct class is class 2, and your model predicted probabilities of [0.7, 0.2, 0.1]. The cross-entropy loss will strongly penalize this because the model placed high confidence on the wrong class.
🔗 Why Softmax and Cross-Entropy Work Well Together
Softmax ensures that outputs are interpretable as probabilities, which is exactly what cross-entropy needs to compare against ground truth labels.
Cross-Entropy Loss then measures how far off the prediction is and gives the model feedback to update its weights through backpropagation.
Together, they form the backbone of classification models in deep learning.
💻 Coding Example: Softmax + Cross-Entropy
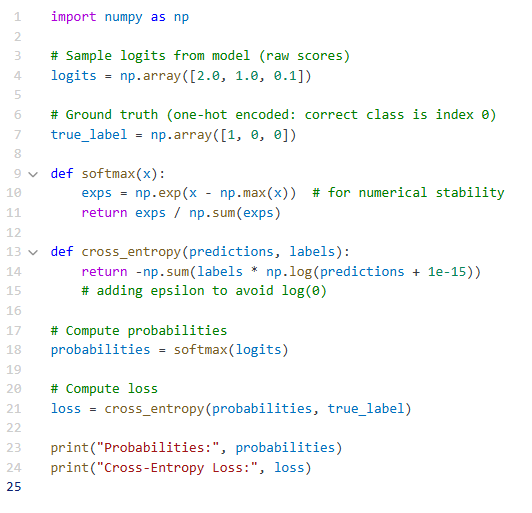

In this example:
- The model is somewhat confident in the correct class.
- The cross-entropy loss reflects that it’s not perfect, but not terrible either.
🚀 Wrapping Up
Softmax gives us probabilities.
Cross-Entropy tells us how good those probabilities are.
These two functions are essential in training classification models — from simple logistic regression to massive models like BERT and GPT. By understanding them, you’re not just tuning models — you're understanding how machines learn to make decisions.