In the context of vector analysis, invariance typically refers to the property of a vector field or mathematical object that remains unchanged under certain transformations. These transformations could be translations, rotations, or scaling. Invariance is important because it ensures that certain properties or behaviors of a system are independent of how the system is viewed or manipulated in space.
Invariance in Vector Analysis
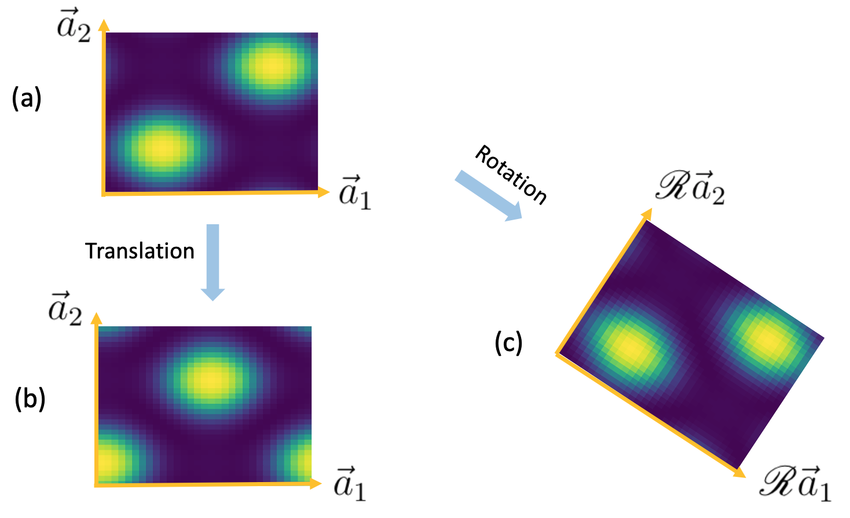
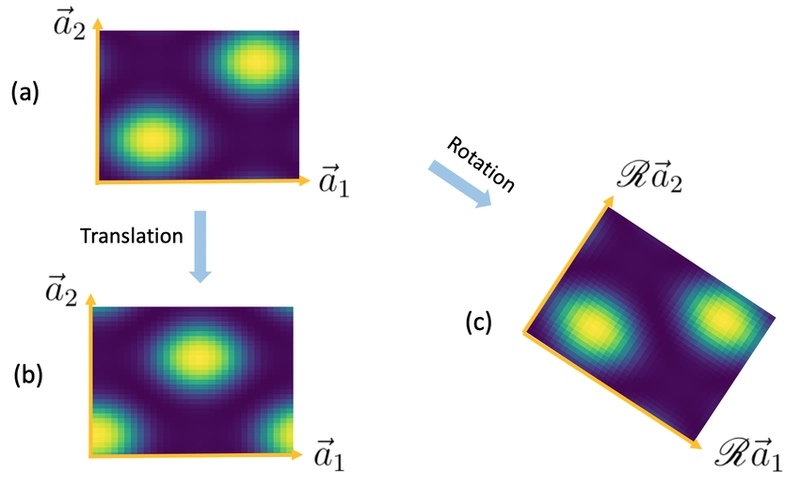
1. Translation Invariance
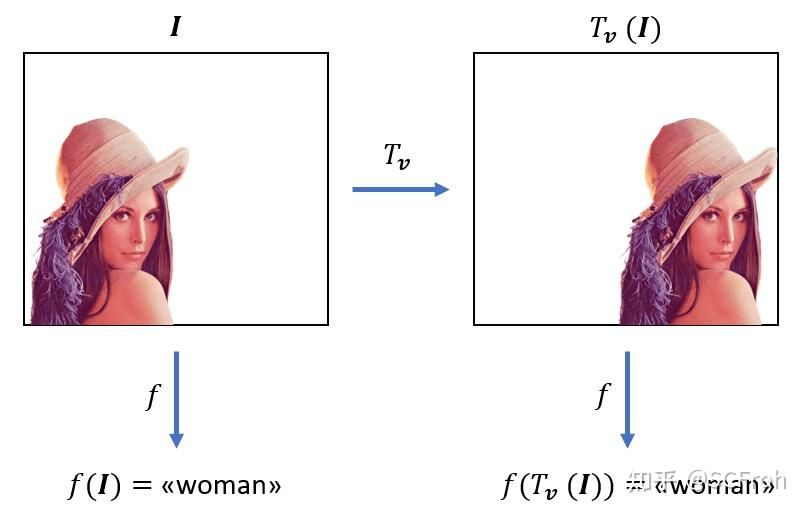
In vector analysis, translation invariance refers to the property that a vector field (such as a force field or velocity field) remains unchanged when the entire system is translated (shifted) in space. This means that the field looks the same at every point in space, regardless of where we "move" the coordinate system.
- Mathematical Formulation: If a vector field ( \mathbf{F}(\mathbf{x}) ) is translated by a vector ( \mathbf{T} ), then the field does not change: [ \mathbf{F}(\mathbf{x} + \mathbf{T}) = \mathbf{F}(\mathbf{x}) ] Translation invariance implies that the physical laws governing the field are the same everywhere, regardless of the reference point.
2. Rotation Invariance
Rotation invariance in vector analysis means that the vector or field does not change when it is rotated around a point or axis. This property is important in many physical situations, such as in electromagnetic fields or fluid dynamics, where the properties of the system remain the same even after a rotation of the coordinate system.
- Mathematical Formulation: If we rotate a vector ( \mathbf{v} ) by a rotation matrix ( \mathbf{R} ), the vector’s direction and magnitude remain unchanged: [ \mathbf{v}' = \mathbf{R} \mathbf{v} ] For a rotation-invariant field, the field remains the same under any rotation. This can be described using the concept of a tensor, which behaves in a predictable way under rotations.
3. Scaling Invariance
Scaling invariance refers to the property that a vector field remains the same if the entire system is scaled (enlarged or reduced) by a factor. This kind of invariance can be useful in systems where the relative properties are more important than the absolute sizes.
- Mathematical Formulation: Scaling a vector field by a constant factor ( \lambda ) should leave the field unchanged: [ \mathbf{F}(\lambda \mathbf{x}) = \lambda \mathbf{F}(\mathbf{x}) ] In physical systems, scaling invariance is seen in phenomena like fractals or in the Navier-Stokes equations for fluid dynamics, where the system behaves similarly regardless of its size.
4. Covariance and Contravariance
In the context of vector analysis, covariance and contravariance describe how vectors transform under coordinate transformations, such as rotations. These concepts help maintain the invariance of physical laws regardless of the choice of coordinate system.
- Covariant vectors (often components of a gradient or derivative) transform in the same way as the coordinate system.
- Contravariant vectors (like position or velocity vectors) transform oppositely to the coordinate system.
5. Example: Invariance of the Dot Product
The dot product is an example of an operation that is invariant under rotation. Given two vectors ( \mathbf{v} ) and ( \mathbf{w} ), the dot product remains the same regardless of the rotation applied to the vectors:
[
\mathbf{v} \cdot \mathbf{w} = \mathbf{R} \mathbf{v} \cdot \mathbf{R} \mathbf{w}
]
This property is crucial in physics, as it ensures that quantities like energy (which are based on dot products) remain consistent regardless of the rotation of the coordinate system.
Summary of Invariance in Vector Analysis
Invariance in vector analysis ensures that certain physical properties or fields remain unchanged under different transformations, which is key to describing the symmetry of physical systems. Some important types of invariance include:
- Translation Invariance: The system remains unchanged when moved.
- Rotation Invariance: The system remains unchanged when rotated.
- Scaling Invariance: The system remains unchanged when scaled.
- Dot Product Invariance: The dot product between vectors remains invariant under rotation.
These concepts are foundational in many fields such as physics, engineering, and machine learning, where understanding the symmetry of systems leads to simpler models and better predictions.