Many game development environments, including Unity, Godot, and Mini Micro, include a lerp function. lerp stands for "Linear Interpolation", and it is easy to define:
lerp = function(x0, x1, t)
return x0 + (x1 - x0) * t
end functionThat is, it just returns a value some fraction t of the way from x0 to x1. (In Mini Micro, you find this in /sys/lib/mathUtil.)
The Crime
Despite its simplicity, it is very common to see people misuse this function. The most frequent abuse looks like this:
x = lerp(x, targetX, dt)where dt is the time step. Seeing x (the value you are updating) as one of the arguments to lerp is unmistakable evidence of the crime. What going on here?
The Effect
If you (ab)use lerp in this way, instead of moving x smoothly from a starting position to a target, you're always moving it some fraction (that depends on the time step) of the way from its current position towards the target. There is nothing linear about it; even if dt is always the same, the amount this moves will depend on how far x is from the target, and will change from frame to frame.
The Motive
Usually when people do something like this, they're think of lerp as a "smoothing" function. They want x to approach targetX, but they don't want it to jump there directly; they want it to sort of smoothly track the target (which is often moving around for other reasons).
The Consequences
This abuse of lerp has several negative consequences:
- It will never actually reach the target.
- ...Unless your time step is bigger than 1 second, in which case it will reach the target instantly (or even overshoot it, depending on whether your lerp function clamps t).
- Any experienced programmer who sees your code and understands lerp will conclude (perhaps unfairly) that you are a noob.
Alternative #1: Use Lerp Properly
The proper way to use lerp is to keep track of the start and end position, and keep those constant, while you pass in a t value that goes from 0 to 1 over time. For example, if you want to reach the target in 1 second, and dt is your time step, you could do:
startX = x
t = 0
while t < 1
yield
t += dt
x = lerp(startX, targetX, t)
end whileWith this code, your x value will move linearly (i.e. at a constant speed) from startX to targetX over one second, and then stop.
Alternative #2: Use moveTowards
Most environments that have lerp also have a moveTowards function. This is somewhat easier to use because you don't have to keep track of the starting position; it also works nicely for a moving target. In Mini Micro, it's defined (also in /sys/lib/mathUtil) this way:
moveTowards = function(num, targetNum, maxChange=1)
if abs(targetNum - num) <= maxChange then return targetNum
if targetNum > num then return num + maxChange
return num - maxChange
end functionThis function moves a value towards a targetValue, but changes no more than maxChange at a time. Unlike lerp, this function really is intended to get the current value (x) as a parameter. You'd use it like this:
x = moveTowards(x, targetX, 20)where that 20 is your speed in pixels per frame (or whatever). Like proper use of lerp, this will move your x towards the target at a constant speed, and then stop.
Often, when people are abusing lerp, it's just because it's inconvenient to keep track of the starting position. Is such cases, moveTowards is probably what they want.
Alternative #3: True Smoothing
If you don't want to move at a constant speed, then you probably want a true smoothing function. This is often used in UI when scrolling, for example — you want your scroll position to change quickly in the middle of its flight, but more slowly at the ends.
When that's what you need, there are a lot of different functions you can choose, with different amounts of smoothing at either end. But a simple trick I like to use is: use lerp, but transform your t value into a sine wave.
With that lerp code above, you would simply change
x = lerp(startX, targetX, t)to:
smoothT = (1 - cos(t*pi)) / 2
x = lerp(startX, targetX, smoothT)That formula for smoothT creates a curve that starts at 0 when t=0, and ends at 1 when t=1... but in between, it is a smooth S-shape curve that starts out slow, accelerates in the middle, and then ends slow.
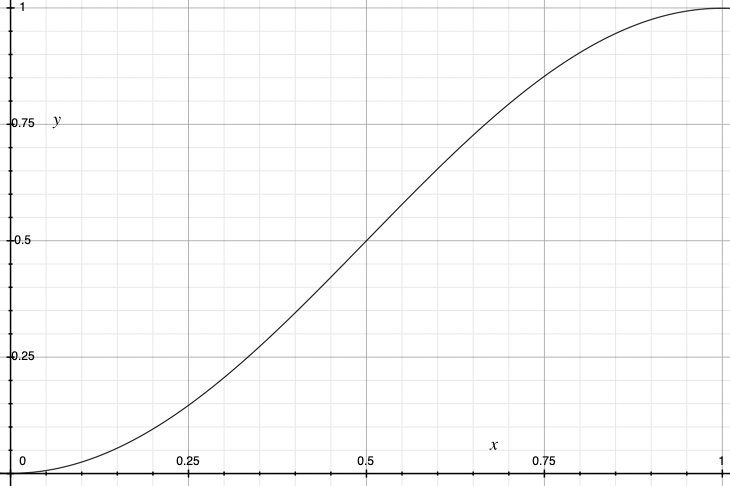
This gives you nice juicy smoothness at either end of the motion, while still retaining all the benefits of lerp:
- It actually reaches the target at the proper time.
- Its behavior doesn't depend on the time step, but only on the absolute time.
- Experienced programmers who see your code will recognize (fairly) that you are a cool frood who really knows how to use
lerp.
Go Forth and Interpolate
Now you know how lerp is used — and abused — you can interpolate values properly wherever you need to do so. Happy coding!